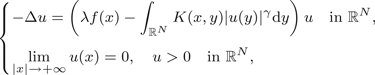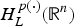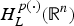Refine search
Actions for selected content:
30 results
Uniqueness of solution for logarithm Choquard equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-29
-
- Article
- Export citation
Existence and uniqueness of a positive solution to a rapidly growing problem via sub-supersolution method
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth solutions to the Christoffel–Minkowski problem in hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-29
-
- Article
- Export citation
On mixed local–nonlocal problems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-34
-
- Article
- Export citation
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1747-1791
- Print publication:
- October 2025
-
- Article
- Export citation
Groundstates of the planar Schrödinger–Poisson system with potential well and lack of symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 993-1023
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solvability for Pucci-Lane-Emden systems in annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 494-507
- Print publication:
- April 2024
-
- Article
- Export citation
Stationary solutions to the Keller–Segel equation on curved planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 327-343
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On sectoriality of degenerate elliptic operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 18 August 2021, pp. 689-710
-
- Article
- Export citation
A continuum limit for the PageRank algorithm
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 April 2021, pp. 472-504
-
- Article
-
- You have access
- Open access
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
ESTIMATES AND RIGIDITY FOR STABLE SOLUTIONS TO SOME NONLINEAR ELLIPTIC PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 10 September 2020, pp. 335-337
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Decay rates at infinity for solutions to periodic Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1113-1126
- Print publication:
- June 2020
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
A quantitative Carleman estimate for second-order elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 915-938
- Print publication:
- August 2019
-
- Article
- Export citation
RECOVERY OF NON-COMPACTLY SUPPORTED COEFFICIENTS OF ELLIPTIC EQUATIONS ON AN INFINITE WAVEGUIDE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1573-1600
- Print publication:
- September 2020
-
- Article
- Export citation
Existence of a Solution for a Non-Local Problem in ℝN via Bifurcation Theory
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 825-845
-
- Article
- Export citation
Variable Hardy Spaces Associated with Operators Satisfying Davies–Gaffney Estimates
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 759-810
-
- Article
- Export citation
The Lane–Emden equation in strips
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 November 2017, pp. 51-62
- Print publication:
- February 2018
-
- Article
- Export citation