Let 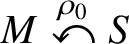 $M\stackrel {\rho _0}{\curvearrowleft }S$ be a
$M\stackrel {\rho _0}{\curvearrowleft }S$ be a 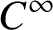 $C^\infty $ locally free action of a connected simply connected solvable Lie group S on a closed manifold M. Roughly speaking,
$C^\infty $ locally free action of a connected simply connected solvable Lie group S on a closed manifold M. Roughly speaking, 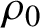 $\rho _0$ is parameter rigid if any
$\rho _0$ is parameter rigid if any 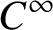 $C^\infty $ locally free action of S on M having the same orbits as
$C^\infty $ locally free action of S on M having the same orbits as 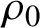 $\rho _0$ is
$\rho _0$ is 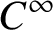 $C^\infty $ conjugate to
$C^\infty $ conjugate to 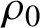 $\rho _0$. In this paper we prove two types of result on parameter rigidity.
$\rho _0$. In this paper we prove two types of result on parameter rigidity.
First let G be a connected semisimple Lie group with finite center of real rank at least 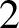 $2$ without compact factors nor simple factors locally isomorphic to
$2$ without compact factors nor simple factors locally isomorphic to 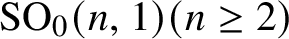 $\mathop {\mathrm {SO}}\nolimits _0(n,1)(n\,{\geq}\, 2)$ or
$\mathop {\mathrm {SO}}\nolimits _0(n,1)(n\,{\geq}\, 2)$ or 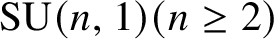 $\mathop {\mathrm {SU}}\nolimits (n,1)(n\geq 2)$, and let
$\mathop {\mathrm {SU}}\nolimits (n,1)(n\geq 2)$, and let  $\Gamma $ be an irreducible cocompact lattice in G. Let
$\Gamma $ be an irreducible cocompact lattice in G. Let 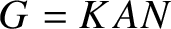 $G=KAN$ be an Iwasawa decomposition. We prove that the action
$G=KAN$ be an Iwasawa decomposition. We prove that the action  $\Gamma \backslash G\curvearrowleft AN$ by right multiplication is parameter rigid. One of the three main ingredients of the proof is the rigidity theorems of Pansu, and Kleiner and Leeb on the quasi-isometries of Riemannian symmetric spaces of non-compact type.
$\Gamma \backslash G\curvearrowleft AN$ by right multiplication is parameter rigid. One of the three main ingredients of the proof is the rigidity theorems of Pansu, and Kleiner and Leeb on the quasi-isometries of Riemannian symmetric spaces of non-compact type.
Secondly we show that if 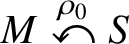 $M\stackrel {\rho _0}{\curvearrowleft }S$ is parameter rigid, then the zeroth and first cohomology of the orbit foliation of
$M\stackrel {\rho _0}{\curvearrowleft }S$ is parameter rigid, then the zeroth and first cohomology of the orbit foliation of 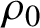 $\rho _0$ with certain coefficients must vanish. This is a partial converse to the results in the author’s [Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups. Geom. Topol. 21(1) (2017), 157–191], where we saw sufficient conditions for parameter rigidity in terms of vanishing of the first cohomology with various coefficients.
$\rho _0$ with certain coefficients must vanish. This is a partial converse to the results in the author’s [Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups. Geom. Topol. 21(1) (2017), 157–191], where we saw sufficient conditions for parameter rigidity in terms of vanishing of the first cohomology with various coefficients.
 $3$-manifolds
$3$-manifolds
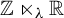 ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on
${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on  ${\mathbb{T}}^{2}$
${\mathbb{T}}^{2}$
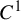 $C^1$-actions on tori
$C^1$-actions on tori
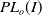 $PL_o(I)$
$PL_o(I)$
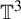 ${\mathbb T}^3$: rigidity versus triviality
${\mathbb T}^3$: rigidity versus triviality