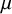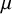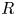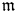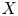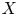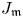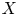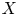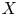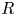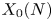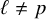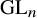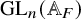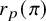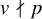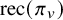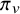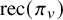Refine search
Actions for selected content:
120 results
COHOMOLOGY OF THE BASIC UNRAMIFIED PEL UNITARY RAPOPORT-ZINK SPACE OF SIGNATURE
 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Likely intersections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 December 2025, e199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-SEMI-STABLE LOCI IN HECKE STACKS AND FARGUES’ CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON INTEGRAL LOCAL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 14 October 2025, pp. 1-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the weak Harder–Narasimhan stratification on
 $B_{\mathrm{dR}}^+$-affine Grassmannian
$B_{\mathrm{dR}}^+$-affine Grassmannian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 15 December 2025, pp. 2654-2711
- Print publication:
- October 2025
-
- Article
- Export citation
F-zips with additional structure on splitting models of Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 September 2025, e142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semi-stable and splitting models for unitary Shimura varieties over ramified places. I.
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of arithmetic special divisors for unitary Shimura varieties (with an appendix by Yujie Xu)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Canonical integral models for Shimura varieties of abelian type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation theory for prismatic G-displays
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear AFL for quaternion algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-23
-
- Article
- Export citation
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
Control theorems for Hilbert modular varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 530-549
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mod p points on shimura varieties of parahoric level
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Attractors are not algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1073-1100
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular curves and Néron models of generalized Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 945-981
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local-global compatibility for regular algebraic cuspidal automorphic representations when
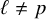 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 12 February 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation