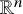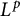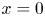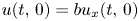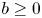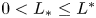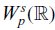Refine search
Actions for selected content:
66 results
RENORMALIZED AND ENTROPY SOLUTIONS TO THE GENERAL NONLINEAR PARABOLIC EQUATIONS IN MUSIELAK–ORLICZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-30
-
- Article
- Export citation
On a Cahn–Hilliard equation for the growth and division of chemically active droplets modelling protocells
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics for the generalised chemotaxis-Navier–Stokes system in
 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling wave solutions and spreading speeds for a scalar age-structured equation with nonlocal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 856-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WELL-POSEDNESS RESULTS FOR GENERAL REACTION–DIFFUSION TRANSPORT OF OXYGEN IN ENCAPSULATED CELLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 154-163
- Print publication:
- February 2025
-
- Article
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 40-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On determining and breaking the gauge class in inverse problems for reaction-diffusion equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 December 2023, pp. 118-148
- Print publication:
- February 2025
-
- Article
- Export citation
Anisotropic flow, entropy, and
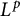 $L^p$-Minkowski problem
$L^p$-Minkowski problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-20
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised solution to a 2D parabolic-parabolic chemotaxis system for urban crime: Global existence and large-time behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 409-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sliding methods for tempered fractional parabolic problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1358-1378
- Print publication:
- August 2024
-
- Article
- Export citation
Effect of the location of a protection zone in a reaction–diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1095-1117
- Print publication:
- August 2024
-
- Article
- Export citation
Uniform bound on the number of partitions for optimal configurations of the Ohta–Kawasaki energy in 3D
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1341-1353
- Print publication:
- December 2023
-
- Article
- Export citation
The stability analysis of a 2D Keller–Segel–Navier–Stokes system in fast signal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 160-209
-
- Article
-
- You have access
- HTML
- Export citation
On the global existence and qualitative behaviour of one-dimensional solutions to a model for urban crime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 919-959
-
- Article
- Export citation
On travelling wave solutions of a model of a liquid film flowing down a fibre
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 12 August 2021, pp. 864-893
-
- Article
- Export citation
On regularity properties of a surface growth model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1869-1892
- Print publication:
- December 2021
-
- Article
- Export citation
Local well-posedness for Frémond’s model of complete damage in elastic solids
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 01 March 2021, pp. 309-327
-
- Article
- Export citation
Well-posedness of the Muskat problem in subcritical Lp-Sobolev spaces
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 224-266
-
- Article
- Export citation
The convergence rate of the fast signal diffusion limit for a Keller–Segel–Stokes system with large initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1972-2012
- Print publication:
- December 2021
-
- Article
- Export citation