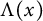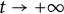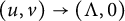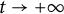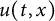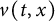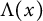Refine search
Actions for selected content:
104 results
Propagation dynamics of time-dependent reaction-diffusion equations under climate change in an infinite cylinder
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of birth pulse and environment shift on population survival and propagation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-27
-
- Article
- Export citation
Global dynamics of a degenerate reaction-diffusion cholera model with phage-bacteria interaction in a heterogeneous environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence-uniqueness theory and small-data decay for a reaction-diffusion model of wildfire spread
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1347-1358
- Print publication:
- December 2025
-
- Article
- Export citation
A free boundary problem of competition-diffusion system with Dirichlet boundary condition
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-20
-
- Article
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 2. The initial-boundary value problem on a finite domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DELAYED HOPF BIFURCATIONS IN REACTION–DIFFUSION SYSTEMS IN TWO SPACE DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1160-1182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal dynamics of a lattice prey–predator system with non-local diffusion in a periodic habitat
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-43
-
- Article
- Export citation
Impact of prey-taxis on a harvested intraguild predation predator–prey model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1183-1220
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A critical non-homogeneous heat equation with weighted source
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 06 March 2025, pp. 1148-1159
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global well-posedness and Turing–Hopf bifurcation of prey-taxis systems with hunting cooperation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1121-1147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis of a model describing bacterial colony expansion in radial geometry driven by chemotaxis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 910-947
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global well-posedness and uniform boundedness of 2D urban crime models with nonlinear advection enhancement
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 897-909
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global existence of a weak solution for a reaction–diffusion system in a porous medium with membrane conditions and mass control
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 2006-2028
- Print publication:
- December 2025
-
- Article
- Export citation
Fractional order for the transmission dynamics of coffee berry diseases (CBD)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 879-896
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 1. The Cauchy problem on the real line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 October 2024, pp. 775-810
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WELL-POSEDNESS RESULTS FOR GENERAL REACTION–DIFFUSION TRANSPORT OF OXYGEN IN ENCAPSULATED CELLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 154-163
- Print publication:
- February 2025
-
- Article
- Export citation
Travelling wavefronts for the Belousov–Zhabotinsky system with non-local delayed interaction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 738-774
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stabilization in a chemotaxis system modelling T-cell dynamics with simultaneous production and consumption of signals
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 570-583
-
- Article
-
- You have access
- Open access
- HTML
- Export citation