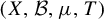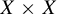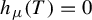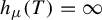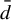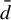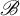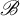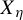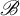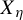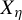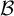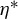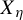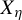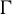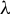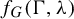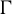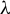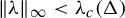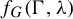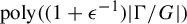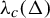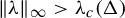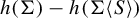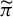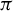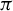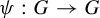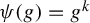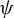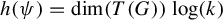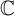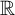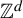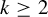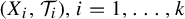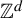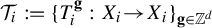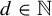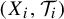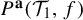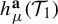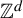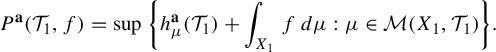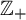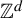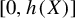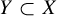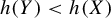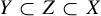Refine search
Actions for selected content:
54 results
Entropy stability and Milnor–Thurston invariants for Bowen–Series-like maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shadowing, sensitivity, and entropy points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 September 2025, pp. 1-17
-
- Article
- Export citation
Variational principles of metric mean dimension for random dynamical systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 September 2025, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
A variational principle of scaled entropy for amenable group actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-28
-
- Article
- Export citation
Some remarks about self-products and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2183-2193
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological and metric emergence of continuous maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 525-551
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal and proximal examples of
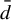 $\bar {d}$-stable and
$\bar {d}$-stable and 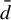 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 396-426
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
Invariant measures for
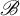 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 2901-2932
- Print publication:
- October 2024
-
- Article
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 2960-2974
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy bounds for multi-word perturbations of subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 665-673
- Print publication:
- February 2024
-
- Article
- Export citation
Relative uniformly positive entropy of induced amenable group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 569-593
- Print publication:
- February 2024
-
- Article
- Export citation
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
A characterization of Thurston’s Master Teapot
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 3354-3382
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 102-111
- Print publication:
- February 2023
-
- Article
- Export citation
A variational principle for weighted topological pressure under
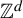 $\mathbb {Z}^{d}$-actions
$\mathbb {Z}^{d}$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 3311-3340
- Print publication:
- October 2023
-
- Article
- Export citation
Subsystem entropies of shifts of finite type and sofic shifts on countable amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 2881-2914
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Garden of Eden and weakly periodic points for certain expansive actions of groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 2354-2375
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy pair realization
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 2471-2488
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation