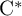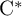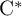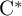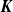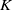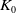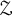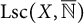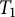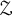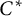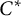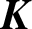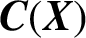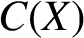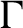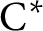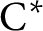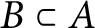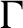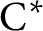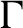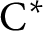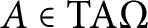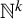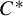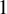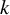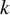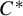Refine search
Actions for selected content:
51 results
Uniform property
 $ \Gamma $ and finite dimensional tracial boundaries
$ \Gamma $ and finite dimensional tracial boundaries
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
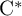 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensorially absorbing inclusions of C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1315-1346
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary groups,
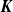 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 229-251
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

The Classical–Quantum Correspondence
-
- Published online:
- 16 December 2022
- Print publication:
- 19 January 2023
-
- Element
- Export citation
Colored isomorphism of classifiable C
 $^*$-algebras
$^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 216-245
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double relative commutants in coronas of separable C*-algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 345-355
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Cuntz semigroup of unital commutative AI-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 1831-1868
- Print publication:
- December 2023
-
- Article
- Export citation
A correspondence between inverse subsemigroups, open wide subgroupoids and cartan intermediate C*-subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 October 2022, pp. 861-879
-
- Article
- Export citation
The generator rank of subhomogeneous
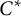 $C^*\!$-algebras
$C^*\!$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1314-1342
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATIONAL
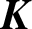 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 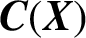 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 119-144
- Print publication:
- August 2023
-
- Article
- Export citation
Uniform property
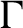 $\Gamma $ for certain
$\Gamma $ for certain 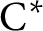 $\mathrm {C^*}$-algebras
$\mathrm {C^*}$-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1063-1070
- Print publication:
- December 2022
-
- Article
- Export citation
Cocycles on groupoids arising from
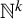 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
C*-algebras where every element is a limit of products of positive elements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 628-632
- Print publication:
- September 2022
-
- Article
- Export citation
A GENERALISATION OF HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 257-266
- Print publication:
- April 2022
-
- Article
- Export citation
INVARIANT SETS AND NORMAL SUBGROUPOIDS OF UNIVERSAL ÉTALE GROUPOIDS INDUCED BY CONGRUENCES OF INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 April 2021, pp. 99-118
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation

Higher Index Theory
-
- Published online:
- 11 June 2020
- Print publication:
- 02 July 2020