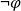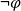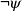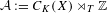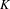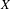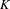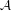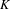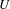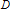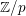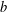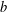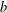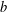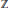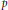Refine search
Actions for selected content:
21 results
Complete Artworks without Authors
-
- Journal:
- Canadian Journal of Philosophy / Volume 53 / Issue 7-8 / October 2023
- Published online by Cambridge University Press:
- 14 May 2024, pp. 666-677
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Human Conditional Reasoning in Answer Set Programming
-
- Journal:
- Theory and Practice of Logic Programming / Volume 24 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 157-192
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
‘I Will Complete a New Covenant’ (Heb 8.8): Christology and New Creation in Hebrews
-
- Journal:
- New Testament Studies / Volume 69 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 230-234
- Print publication:
- April 2023
-
- Article
- Export citation
Positive Dependency Graphs Revisited
-
- Journal:
- Theory and Practice of Logic Programming / Volume 23 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1128-1137
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Monoidal Structures
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 234-316
-
- Chapter
- Export citation
Predictors of engagement and outcome achievement in a behavioural intervention targeting sugar-sweetened beverage intake among rural adults
-
- Journal:
- Public Health Nutrition / Volume 23 / Issue 3 / February 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 554-563
-
- Article
-
- You have access
- HTML
- Export citation
Sylvester matrix rank functions on crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 2913-2946
- Print publication:
- November 2020
-
- Article
- Export citation

Slenderness
-
- Published online:
- 30 November 2018
- Print publication:
- 06 December 2018
Uniqueness of the von Neumann Continuous Factor
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-982
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
On discrete homology of a free pro-
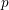 $p$-group
$p$-group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 07 September 2018, pp. 2195-2204
- Print publication:
- October 2018
-
- Article
- Export citation
ON THE COMPLETION OF
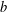 $b$-METRIC SPACES
$b$-METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 298-304
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Preparation for the end of life and life completion during late-stage lung cancer: An exploratory analysis
-
- Journal:
- Palliative & Supportive Care / Volume 15 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 554-564
-
- Article
- Export citation
Unmarried patients with early cognitive impairment are more likely than their married counterparts to complete advance care plans
-
- Journal:
- International Psychogeriatrics / Volume 29 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 509-516
-
- Article
- Export citation
Coherent presentations of Artin monoids
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 957-998
- Print publication:
- May 2015
-
- Article
- Export citation
Lloyd-Topor completion and general stable models
-
- Journal:
- Theory and Practice of Logic Programming / Volume 13 / Issue 4-5 / July 2013
- Published online by Cambridge University Press:
- 25 September 2013, pp. 503-515
-
- Article
- Export citation
Non-dieting group interventions for overweight and obese women: what predicts non-completion and does completion improve outcomes?
-
- Journal:
- Public Health Nutrition / Volume 13 / Issue 10 / October 2010
- Published online by Cambridge University Press:
- 22 December 2009, pp. 1622-1628
-
- Article
-
- You have access
- HTML
- Export citation
Maximal immediate extensions are not necessarily maximally complete
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 196-211
-
- Article
-
- You have access
- Export citation
Finite Completion of comma-free codesPart 1
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 38 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 15 June 2004, pp. 91-115
- Print publication:
- April 2004
-
- Article
- Export citation
Finite Completion of comma-free codes Part 2
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 38 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 15 June 2004, pp. 117-136
- Print publication:
- April 2004
-
- Article
- Export citation
Adic Topologies for the Rational Integers
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 4 / 01 August 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 711-723
- Print publication:
- 01 August 2003
-
- Article
-
- You have access
- Export citation