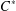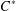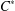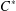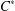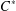Refine search
Actions for selected content:
22 results
Simplicity of crossed products by FC-hypercentral groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 28 October 2025, pp. 2272-2319
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Background
- from Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 3-49
-
- Chapter
- Export citation
2 - Lie groups and coadjoint orbits
- from Part I - Mathematical background
-
- Book:
- Quantum Geometry, Matrix Theory, and Gravity
- Published online:
- 04 April 2024
- Print publication:
- 11 April 2024, pp 13-28
-
- Chapter
- Export citation
Substreetutions and more on trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 2399-2453
- Print publication:
- September 2024
-
- Article
- Export citation
Global rigidity of higher rank lattice actions with dominated splitting
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 799-828
- Print publication:
- March 2024
-
- Article
- Export citation
Abstract almost periodicity for group actions on uniform topological spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 798-829
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free rank of symmetry of products of Dold manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 March 2023, pp. 117-132
-
- Article
- Export citation
ON LARGE ORBITS OF FINITE SOLVABLE GROUPS ON CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 438-442
- Print publication:
- December 2023
-
- Article
- Export citation
4 - The Lorentz Group and the Poincaré Group
- from PART I - Basics
-
- Book:
- What Is a Quantum Field Theory?
- Published online:
- 22 February 2022
- Print publication:
- 17 March 2022, pp 102-131
-
- Chapter
- Export citation
We the People: Is the Polity the State?
-
- Journal:
- Journal of the American Philosophical Association / Volume 7 / Issue 1 / Spring 2021
- Published online by Cambridge University Press:
- 22 February 2021, pp. 78-97
-
- Article
- Export citation
MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 66-77
- Print publication:
- August 2021
-
- Article
- Export citation
The Implementation of Collective Redress – A Comparative Approach
-
- Journal:
- German Law Journal / Volume 21 / Issue 8 / December 2020
- Published online by Cambridge University Press:
- 01 December 2020, pp. 1606-1624
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Comment on Ergodic Theorem for Amenable Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 257-261
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Actions of Semitopological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 441-450
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A NEW MENON’S IDENTITY FROM GROUP ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 369-375
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
IDEAL CHAINS IN RESIDUALLY FINITE DEDEKIND DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 56-67
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Orbifold Zeta Functions for Dual Invertible Polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 May 2016, pp. 99-106
-
- Article
- Export citation
GROUP ACTION PRESERVING THE HAAGERUP PROPERTY OF
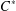 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 August 2015, pp. 295-300
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Cumulants and partition lattices III: Multiply-indexed arrays
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-182
-
- Article
-
- You have access
- Export citation


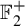
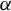
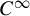
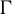
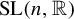
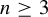
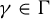
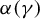
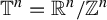
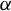
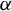
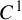
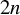
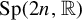
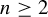
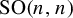
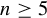
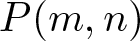
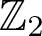
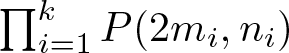
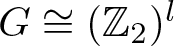
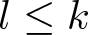
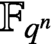
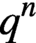
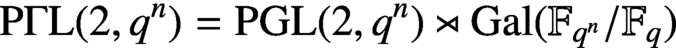
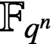

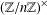
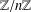
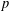

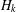
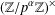
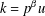

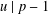
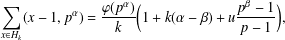
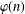
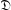

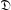
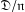
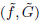 . Here we study the reduced orbifold zeta functions of dual pairs (
. Here we study the reduced orbifold zeta functions of dual pairs (