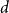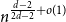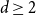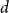Refine search
Actions for selected content:
48569 results in Computer Science
Emerging trends: evaluating general purpose foundation models
-
- Journal:
- Natural Language Engineering / Volume 30 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1323-1335
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Legal Safeguards in the EU Legal Order
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp 230-296
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Abbreviations
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp xxiii-xxiv
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Preface
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp xv-xvi
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Illustrations of Algorithmic Regulation
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp xiii-xiv
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Table of Cases
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp xix-xxii
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
3 - The Rule of Law
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp 95-150
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Bibliography
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp 311-344
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
A review of methods for mapping 3D rotations to one-dimensional planar rotations: analysis, comparison, and a novel efficient Quaternion-based approach
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Copyright page
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp iv-iv
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
 $\gamma $-ADMISSIBILITY IN FIRST-ORDER RELEVANT LOGICS: PROOF USING NORMAL MODELS IN THE MARES–GOLDBLATT SETTING
$\gamma $-ADMISSIBILITY IN FIRST-ORDER RELEVANT LOGICS: PROOF USING NORMAL MODELS IN THE MARES–GOLDBLATT SETTING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 398-419
- Print publication:
- June 2025
-
- Article
- Export citation
Detailed Contents
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp vii-x
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Acknowledgements
-
- Book:
- Algorithmic Rule By Law
- Published online:
- 14 December 2024
- Print publication:
- 12 December 2024, pp xvii-xviii
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
An example of goal-directed, calculational proof
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 34 / 2024
- Published online by Cambridge University Press:
- 11 December 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twin-width of sparse random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 401-420
-
- Article
- Export citation
Bottom-up computation using trees of sublists
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 34 / 2024
- Published online by Cambridge University Press:
- 11 December 2024, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Social impact evaluation analysis: a systematic qualitative method for assessing engineered products
- Part of
-
- Journal:
- Design Science / Volume 10 / 2024
- Published online by Cambridge University Press:
- 11 December 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ChatGPT in foreign language lesson plan creation: Trends, variability, and historical biases
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tight bound for the Erdős–Pósa property of tree minors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 321-325
-
- Article
- Export citation
Affective Matter: designing human-material interactions to enhance health and wellbeing
-
- Journal:
- Design Science / Volume 10 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation



 of a wide range of propositional relevant logics for which excluded middle is valid (with fusion and the Ackermann truth constant), the first-order extensions
of a wide range of propositional relevant logics for which excluded middle is valid (with fusion and the Ackermann truth constant), the first-order extensions  and
and  admit
admit