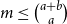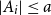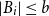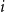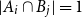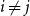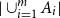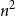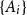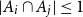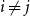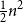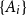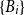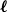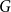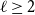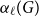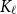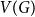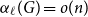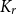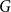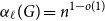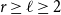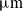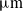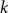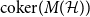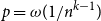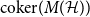Refine search
Actions for selected content:
48287 results in Computer Science
Distributed Subweb Specifications for Traversing the Web
-
- Journal:
- Theory and Practice of Logic Programming / Volume 24 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 394-420
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHAT MODEL COMPANIONSHIP CAN SAY ABOUT THE CONTINUUM PROBLEM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 546-585
- Print publication:
- June 2024
-
- Article
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A physics-based domain adaptation framework for modeling and forecasting building energy systems
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Operationalizing digital self-determination
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clique-factors in graphs with sublinear
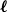 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 665-681
-
- Article
- Export citation
Design and optimization of a decoupled serial constant force microgripper for force sensitive objects manipulation
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expected number of faces in a random embedding of any graph is at most linear
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 682-690
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Open data as an anticorruption tool? Using distributed cognition to understand breakdowns in the creation of transparency data
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Idea evaluation as a design process: understanding how experts develop ideas and manage fixations
-
- Journal:
- Design Science / Volume 9 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introduction to the Special Issue on Logic Rules and Reasoning: Selected Papers from the 4th International Joint Conference on Rules and Reasoning (RuleML+RR 2020)
-
- Journal:
- Theory and Practice of Logic Programming / Volume 23 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 503-506
-
- Article
-
- You have access
- HTML
- Export citation
Index
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 251-256
-
- Chapter
- Export citation
List of Notation
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp ix-x
-
- Chapter
- Export citation
8 - Theory of Computation
- from Part II - Solutions
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 193-249
-
- Chapter
- Export citation
Probabilistic selection and design of concrete using machine learning
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 20 April 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation