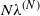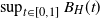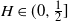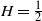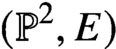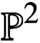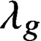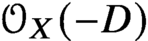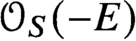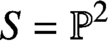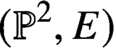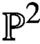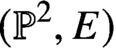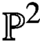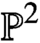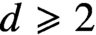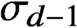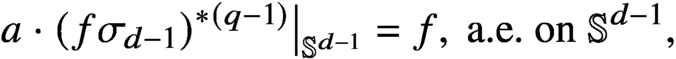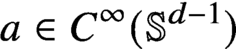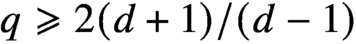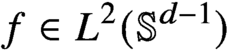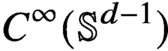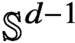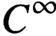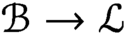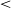Refine listing
Actions for selected content:
38 results in Journal Articles Collection MAT
Parabolic coordinates
-
- Journal:
- The Mathematical Gazette / Volume 105 / Issue 563 / July 2021
- Published online by Cambridge University Press:
- 21 June 2021, pp. 226-236
- Print publication:
- July 2021
-
- Article
- Export citation
On the frequency of Friday the thirteenth
-
- Journal:
- The Mathematical Gazette / Volume 105 / Issue 563 / July 2021
- Published online by Cambridge University Press:
- 21 June 2021, pp. 222-225
- Print publication:
- July 2021
-
- Article
- Export citation
Review of the direct derivation method: quantitative phase analysis with observed intensities and chemical composition data
-
- Journal:
- Powder Diffraction / Volume 36 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 18 June 2021, pp. 159-168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sensitivity of mean-field fluctuations in Erlang loss models with randomized routing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 428-448
- Print publication:
- June 2021
-
- Article
- Export citation
Continuum line-of-sight percolation on Poisson–Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 510-536
- Print publication:
- June 2021
-
- Article
- Export citation
Ruin problems for epidemic insurance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 484-509
- Print publication:
- June 2021
-
- Article
- Export citation
Bounds for expected supremum of fractional Brownian motion with drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 411-427
- Print publication:
- June 2021
-
- Article
- Export citation
Holomorphic anomaly equation for
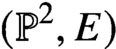 $({\mathbb P}^2,E)$ and the Nekrasov-Shatashvili limit of local
$({\mathbb P}^2,E)$ and the Nekrasov-Shatashvili limit of local 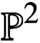 ${\mathbb P}^2$
${\mathbb P}^2$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 May 2021, e3
-
- Article
-
- You have access
- Open access
- Export citation
Smoothness of solutions of a convolution equation of restricted type on the sphere
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 April 2021, e12
-
- Article
-
- You have access
- Open access
- Export citation
Uniformly factoring weakly compact operators and parametrised dualisation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e22
-
- Article
-
- You have access
- Open access
- Export citation
Human–agent transfer from observations
-
- Journal:
- The Knowledge Engineering Review / Volume 36 / 2021
- Published online by Cambridge University Press:
- 27 November 2020, e2
-
- Article
- Export citation
Is p-value
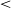 $<$ 0.05 enough? A study on the statistical evaluation of classifiers
$<$ 0.05 enough? A study on the statistical evaluation of classifiers
-
- Journal:
- The Knowledge Engineering Review / Volume 36 / 2021
- Published online by Cambridge University Press:
- 27 November 2020, e1
-
- Article
- Export citation
Self-magnetic field effects on laser-driven wakefield electron acceleration in axially magnetized ion channel
-
- Journal:
- Laser and Particle Beams / Volume 38 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 222-228
-
- Article
- Export citation
A laser-driven droplet source for plasma physics applications
-
- Journal:
- Laser and Particle Beams / Volume 38 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 11 September 2020, pp. 214-221
-
- Article
- Export citation
Study on Plate Straightening Process Based on Elastic-Plastic B Spline Finite Strip Method
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 737-747
- Print publication:
- December 2020
-
- Article
- Export citation
Investigation of Bending Stiffness of Gas Turbine Engine Rotor Flanged Connection
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 729-736
- Print publication:
- December 2020
-
- Article
- Export citation