Refine listing
Actions for selected content:
264 results in 14Cxx
Brill-Noether loci of pencils with prescribed ramification on moduli of curves and on severi varieties on
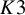 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 22 January 2026, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noether-Lefschetz cycles on the moduli space of abelian varieties
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 14 / 2026
- Published online by Cambridge University Press:
- 13 January 2026, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the rationality problem for low degree hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 December 2025, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-crossing integral chow rings of
 ${\overline {\mathcal {M}}}_{1,n\leq 4}$
${\overline {\mathcal {M}}}_{1,n\leq 4}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e196
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
J-INVARIANT OF LINEAR ALGEBRAIC GROUPS OF OUTER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-28
-
- Article
- Export citation
Optimal bound for singularities on Fano type fibrations of relative dimension one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 November 2025, e193
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit formulas for the Grothendieck class of
 $\overline {\mathcal{M}}_{0,n}$
$\overline {\mathcal{M}}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Seshadri constants on
 $\mathbb {P}^1\times \mathbb {P}^1$ and applications to the symplectic packing problem
$\mathbb {P}^1\times \mathbb {P}^1$ and applications to the symplectic packing problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 November 2025, e191
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Initial degenerations of flag varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 10 November 2025, pp. 1-29
-
- Article
- Export citation
Vanishing criteria for Ceresa cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 29 December 2025, pp. 3017-3043
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in
 $\mathbb{C}^2$
$\mathbb{C}^2$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hodge theory of abelian covers of algebraic varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e159
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Rank of the Normal Functions of the Ceresa and Gross–Schoen Cycles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 September 2025, e141
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Nori and Hodge realisations of Voevodsky motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 2155-2201
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant vector bundles on toric schemes over semirings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORSION BIRATIONAL MOTIVES OF SURFACES AND UNRAMIFIED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2283-2315
- Print publication:
- November 2025
-
- Article
- Export citation
Morava J-invariant
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 July 2025, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHERENCE OF MULTIPLIER SUBMODULE SHEAVES ON GENERIC COMPLEX TORI
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 666-673
-
- Article
- Export citation
Functional Transcendence of Periods and the Geometric André–Grothendieck Period Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation