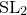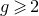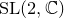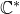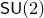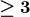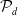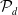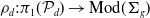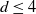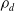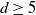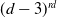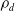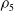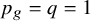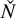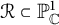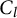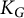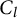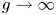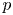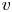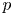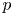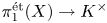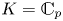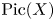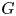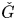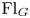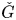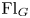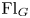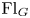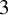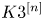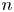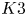Refine listing
Actions for selected content:
240 results in 14Dxx
On families of K3 surfaces with real multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A power structure over the Grothendieck ring of geometric dg categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 05 December 2024, pp. 300-318
-
- Article
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 79-92
- Print publication:
- March 2025
-
- Article
- Export citation
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic and analytic compactifications of the Hitchin moduli space
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KSB stability is automatic in codimension
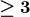 $\boldsymbol{\geq 3}$
$\boldsymbol{\geq 3}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the monodromy group of the family of smooth quintic plane curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 163-184
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periods of elliptic surfaces with
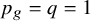 $p_g=q=1$
$p_g=q=1$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
The Atiyah class on algebraic stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 November 2024, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semistable degenerations of Calabi–Yau manifolds and mirror P=W conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Whittaker coefficients of geometric Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flags of sheaves, quivers and symmetric polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On irreducible representations of Fuchsian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 970-990
- Print publication:
- December 2024
-
- Article
- Export citation
Low-degree Hurwitz stacks in the Grothendieck ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1784-1849
- Print publication:
- August 2024
-
- Article
- Export citation
A geometric p-adic Simpson correspondence in rank one
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1433-1466
- Print publication:
- July 2024
-
- Article
- Export citation
Twisted Whittaker category on affine flags and the category of representations of the mixed quantum group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1349-1417
- Print publication:
- June 2024
-
- Article
- Export citation
Deformations of Calabi–Yau varieties with k-liminal singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational Hodge isometries of hyper-Kähler varieties of
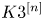 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1261-1303
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation