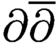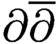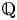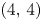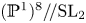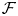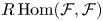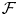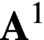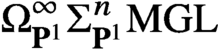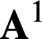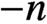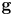Refine listing
Actions for selected content:
257 results in 14Dxx
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD
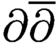 $\partial \overline {\partial }$-LEMMA
$\partial \overline {\partial }$-LEMMA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 305-354
-
- Article
- Export citation
A specialization inequality for tropical complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1051-1078
- Print publication:
- May 2021
-
- Article
- Export citation
Rational points and derived equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1036-1050
- Print publication:
- May 2021
-
- Article
- Export citation
ON THE FIRST STEPS OF THE MINIMAL MODEL PROGRAM FOR THE MODULI SPACE OF STABLE POINTED CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 April 2021, pp. 145-211
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Perverse Leray filtration and specialisation with applications to the Hitchin morphism
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 443-487
- Print publication:
- March 2022
-
- Article
- Export citation
KSBA compactification of the moduli space of K3 surfaces with a purely non-symplectic automorphism of order four
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 99-127
-
- Article
- Export citation
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation
KUMMER COVERINGS AND SPECIALISATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1029-1065
- Print publication:
- May 2022
-
- Article
- Export citation
Minimising CM degree and slope stability of projective varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 125-137
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Formality conjecture for minimal surfaces of Kodaira dimension 0
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 February 2021, pp. 215-235
- Print publication:
- February 2021
-
- Article
- Export citation
Verlinde formulae on complex surfaces: K-theoretic invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e5
-
- Article
-
- You have access
- Open access
- Export citation
Fano quiver moduli
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 984-1000
- Print publication:
- December 2021
-
- Article
- Export citation
Modules over algebraic cobordism
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 17 December 2020, e14
-
- Article
-
- You have access
- Open access
- Export citation
Localizing virtual structure sheaves for almost perfect obstruction theories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 December 2020, e61
-
- Article
-
- You have access
- Open access
- Export citation
Toric degenerations of cluster varieties and cluster duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 07 December 2020, pp. 2149-2206
- Print publication:
- October 2020
-
- Article
- Export citation
Decomposition of degenerate Gromov–Witten invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 19 November 2020, pp. 2020-2075
- Print publication:
- October 2020
-
- Article
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
Instanton sheaves and representations of quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 984-1004
-
- Article
- Export citation
Degeneracy loci, virtual cycles and nested Hilbert schemes II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1623-1663
- Print publication:
- August 2020
-
- Article
- Export citation
Threefolds fibred by mirror sextic double planes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 1305-1346
- Print publication:
- October 2021
-
- Article
- Export citation