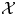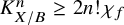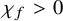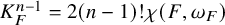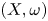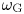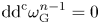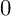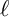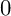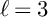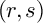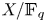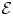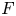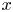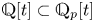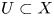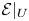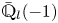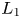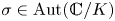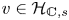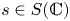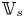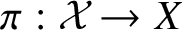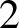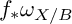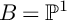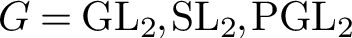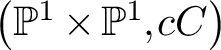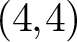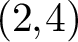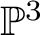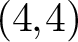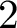Refine listing
Actions for selected content:
239 results in 14Dxx
On birationally trivial families and adjoint quadrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Severi inequality for fibrations of maximal Albanese dimension over curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 June 2022, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singular Gauduchon metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 1314-1328
- Print publication:
- June 2022
-
- Article
- Export citation
THE BOUNDARY OF THE p-RANK
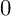 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank 2 local systems and abelian varieties II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 868-892
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute Hodge and ℓ-adic monodromy
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 568-584
- Print publication:
- March 2022
-
- Article
- Export citation
Stringy invariants and toric Artin stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schiffer variations and the generic Torelli theorem for hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 89-122
- Print publication:
- January 2022
-
- Article
- Export citation
Dieudonné theory via cohomology of classifying stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 December 2021, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fundamental local equivalences in quantum geometric Langlands
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 27 December 2021, pp. 2699-2732
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUJITA DECOMPOSITION AND MASSEY PRODUCT FOR FIBERED VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 624-652
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PL DENSITY INVARIANT FOR TYPE II DEGENERATING K3 SURFACES, MODULI COMPACTIFICATION AND HYPER-KÄHLER METRIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 03 November 2021, pp. 574-614
- Print publication:
- September 2022
-
- Article
- Export citation
INTERSECTION COHOMOLOGY OF RANK 2 CHARACTER VARIETIES OF SURFACE GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1615-1654
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-MODULI OF CURVES ON A QUADRIC SURFACE AND K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 16 September 2021, pp. 1251-1291
- Print publication:
- May 2023
-
- Article
- Export citation
Endoscopic decompositions and the Hausel–Thaddeus conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 August 2021, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smoothing toroidal crossing spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 August 2021, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTION COHOMOLOGY OF THE MODULI SPACE OF HIGGS BUNDLES ON A GENUS 2 CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1037-1086
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirabolic Satake equivalence and supergroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 July 2021, pp. 1724-1765
- Print publication:
- August 2021
-
- Article
- Export citation