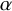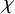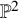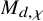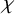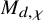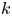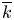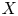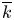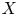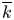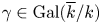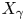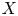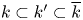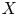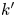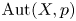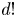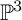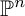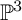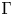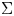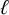Refine listing
Actions for selected content:
239 results in 14Dxx
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 2713-2732
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on quantum K-theory of root constructions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 494-500
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic Beauville’s Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological
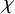 $\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on
$\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on 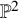 $\mathbb {P}^2$
$\mathbb {P}^2$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fields of moduli and the arithmetic of tame quotient singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 27 March 2024, pp. 982-1003
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Components of moduli stacks of two-dimensional Galois representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Artin algebraization for pairs with applications to the local structure of stacks and Ferrand pushouts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 February 2024, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lie algebra actions on module categories for truncated shifted yangians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heights and quantitative arithmetic on stacky curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 481-534
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drinfeld's lemma for F-isocrystals, II: Tannakian approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 90-119
- Print publication:
- January 2024
-
- Article
- Export citation
On the nilpotent orbit theorem of complex variations of Hodge structure
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 November 2023, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compactifications of moduli of del Pezzo surfaces via line arrangement and K-stability
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2115-2135
- Print publication:
- December 2024
-
- Article
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
Classification of subpencils for hyperplane sections on certain K3 surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1022-1043
-
- Article
- Export citation
NEW MODULI SPACES OF ONE-DIMENSIONAL SHEAVES ON
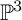 $\mathbb {P}^3$
$\mathbb {P}^3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 265-314
- Print publication:
- June 2024
-
- Article
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
On the period of Li, Pertusi, and Zhao’s symplectic variety
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1432-1453
- Print publication:
- August 2024
-
- Article
- Export citation
Complex multiplication and Noether–Lefschetz loci of the twistor space of a K3 surface
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 17-38
- Print publication:
- January 2024
-
- Article
- Export citation
On Bloch’s map for torsion cycles over non-closed fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 June 2023, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonemptiness of severi varieties on enriques surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 June 2023, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation