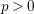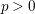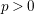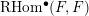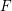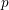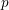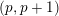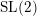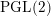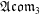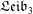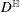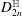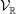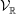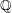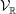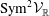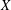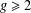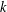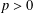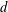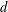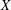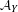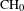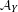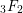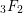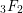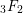Refine listing
Actions for selected content:
239 results in 14Dxx
ON VARIETIES WITH TRIVIAL TANGENT BUNDLE IN CHARACTERISTIC
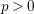 $p>0$
$p>0$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 26 June 2019, pp. 35-51
- Print publication:
- June 2021
-
- Article
- Export citation
ALGEBRAIC SURFACES WITH INFINITELY MANY TWISTOR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 May 2019, pp. 61-70
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
THE KUGA–SATAKE CONSTRUCTION UNDER DEGENERATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 2165-2182
- Print publication:
- November 2020
-
- Article
- Export citation
Autoequivalences of twisted K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 912-937
- Print publication:
- May 2019
-
- Article
- Export citation
Formality conjecture for K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 23 April 2019, pp. 902-911
- Print publication:
- May 2019
-
- Article
- Export citation
NC-smooth algebroid thickenings for families of vector bundles and quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 18 March 2019, pp. 681-710
- Print publication:
- April 2019
-
- Article
- Export citation
On local stabilities of
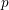 $p$-Kähler structures
$p$-Kähler structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 455-483
- Print publication:
- March 2019
-
- Article
- Export citation
The inertia operator on the motivic Hall algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 14 March 2019, pp. 528-598
- Print publication:
- March 2019
-
- Article
- Export citation
Geometric Langlands correspondence for
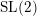 $\text{SL}(2)$,
$\text{SL}(2)$, 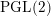 $\text{PGL}(2)$ over the pair of pants
$\text{PGL}(2)$ over the pair of pants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 324-371
- Print publication:
- February 2019
-
- Article
- Export citation
Degenerations of Leibniz and Anticommutative Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 539-549
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
On Deformations of Pairs (Manifold, Coherent Sheaf)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1209-1241
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
The Mod Two Cohomology of the Moduli Space of Rank Two Stable Bundles on a Surface and Skew Schur Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 683-715
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On Motivic Realizations of the Canonical Hermitian Variations of Hodge Structure of Calabi–Yau Type over type
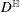 $D^{\mathbb{H}}$ Domains
$D^{\mathbb{H}}$ Domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 209-221
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 195-202
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
FUJITA DECOMPOSITION AND HODGE LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1389-1408
- Print publication:
- July 2020
-
- Article
- Export citation
On a logarithmic version of the derived McKay correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 08 November 2018, pp. 2534-2585
- Print publication:
- December 2018
-
- Article
- Export citation
 $K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION
$K3$ CATEGORIES, ONE-CYCLES ON CUBIC FOURFOLDS, AND THE BEAUVILLE–VOISIN FILTRATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1601-1627
- Print publication:
- September 2020
-
- Article
- Export citation
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION
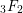 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 29-46
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
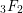 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 July 2018, e12
-
- Article
-
- You have access
- Open access
- Export citation