Refine listing
Actions for selected content:
213 results in 14Exx
NORMAL SPLIT DIVISORS IN RATIONAL HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 12 January 2026, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the rationality problem for low degree hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 December 2025, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal bound for singularities on Fano type fibrations of relative dimension one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 November 2025, e193
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pathological MMP singularities as αp-quotients
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 November 2025, e185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On proper splinters in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 December 2025, pp. 2493-2544
- Print publication:
- October 2025
-
- Article
- Export citation
On the MMP for rank one foliations on threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 25 September 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On semi-ampleness of the moduli part
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECTIVE BOUND FOR SINGULARITIES ON TORIC FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 779-795
-
- Article
-
- You have access
- HTML
- Export citation
Motivic versions of mass formulas by Krasner, Serre and Bhargava
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundedness of slc degenerations of polarized log Calabi–Yau pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 September 2025, e144
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Model Program for Normal Pairs along log Canonical Locus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 September 2025, e143
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal subgroups in the Cremona group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 November 2025, pp. 2442-2460
- Print publication:
- September 2025
-
- Article
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
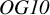 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic singularities and threefold flops in positive characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1188-1244
-
- Article
- Export citation
ON THE DEGREE OF IRRATIONALITY OF LOW GENUS
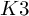 $K3$ SURFACES
$K3$ SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 627-662
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROJECTIVELY FLAT FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 763-812
- Print publication:
- May 2025
-
- Article
- Export citation
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 24 February 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local Normal Forms of Noncommutative Functions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complements and coregularity of Fano varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Covering gonality of symmetric products of curves and Cayley–Bacharach condition on Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
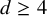
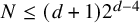
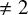
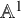
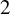













































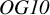



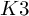



 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 

 of degree
of degree 


























