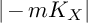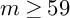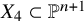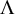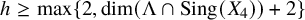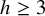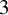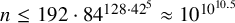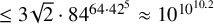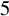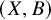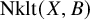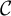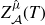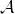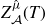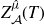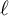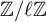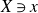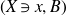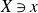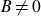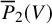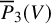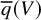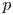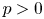Refine listing
Actions for selected content:
213 results in 14Exx
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
-
- Article
- Export citation
Minimal log discrepancies of hypersurface mirrors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 19 February 2024, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
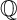 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
-
- Article
- Export citation
Nonsolidity of uniruled varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 August 2023, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quartic and Quintic Hypersurfaces with Dense Rational Points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remark on complements on surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Angehrn-Siu-Helmke’s method applied to abelian varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 May 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the connectedness principle and dual complexes for generalized pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of arcs and comparison of formal neighborhoods for a curve singularity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global Asymptotics of the Sixth Painlevé Equation in Okamoto’s Space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 March 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The existence of the Kähler–Ricci soliton degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 March 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIFORM LOCAL CONSTANCY OF ÉTALE COHOMOLOGY OF RIGID ANALYTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 839-896
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Divisors computing minimal log discrepancies on lc surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 107-128
- Print publication:
- July 2023
-
- Article
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
SEMIAMPLENESS FOR CALABI–YAU SURFACES IN POSITIVE AND MIXED CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 365-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic dynamics of the pentagram map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 3460-3505
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher index Fano varieties with finitely many birational automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 December 2022, pp. 2033-2045
- Print publication:
- November 2022
-
- Article
- Export citation