Refine listing
Actions for selected content:
122 results in 49Jxx
OPTIMAL CONTROL OF MULTIPLE-TIME DELAYED SYSTEMS BASED ON THE CONTROL PARAMETERIZATION METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 1 / July 2011
- Published online by Cambridge University Press:
- 29 May 2012, pp. 68-86
-
- Article
-
- You have access
- Export citation
DOMAIN PERTURBATION FOR PARABOLIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 174-176
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Baire's category in existence problems for non-convex lower semicontinuous evolution differential inclusions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 15 June 2011, pp. 645-667
-
- Article
-
- You have access
- Export citation
Optimal control of stochastic delay equations and time-advanced backward stochastic differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 572-596
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
GENERALIZED IMPLICIT INCLUSION PROBLEMS ON NONCOMPACT SETS WITH APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 261-279
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Infinitely many solutions for a class of systems of differential inclusions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 9-23
-
- Article
-
- You have access
- Export citation
OPTIMAL CONTROL PROBLEMS FOR GENERAL GLOBAL HYBRID DYNAMICAL SYSTEMS WITH MATRIX COST FUNCTIONAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 04 October 2010, pp. 331-349
-
- Article
-
- You have access
- Export citation
AN EFFICIENT COMPUTATIONAL APPROACH TO A CLASS OF MINMAX OPTIMAL CONTROL PROBLEMS WITH APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 20 May 2010, pp. 162-177
-
- Article
-
- You have access
- Export citation
ON AN IMPLICIT HIERARCHICAL FIXED POINT APPROACH TO VARIATIONAL INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 117-124
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
FRÉCHET INTERMEDIATE DIFFERENTIABILITY OF LIPSCHITZ FUNCTIONS ON ASPLUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 309-317
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON PSEUDOMONOTONE SET-VALUED MAPPINGS IN TOPOLOGICAL VECTOR SPACES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 258-265
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS FOR A DIRICHLET PROBLEM WITH p-LAPLACIAN AND SET-VALUED NONLINEARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 285-303
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
GENERALIZED MIXED QUASI-COMPLEMENTARITY PROBLEMS IN TOPOLOGICAL VECTOR SPACES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 525-531
-
- Article
-
- You have access
- Export citation
AN η-APPROXIMATION METHOD FOR NONSMOOTH MULTIOBJECTIVE PROGRAMMING PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 309-323
-
- Article
-
- You have access
- Export citation
Optimal dividend payments until ruin of diffusion processes when payments are subject to both fixed and proportional costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 669-689
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Extremal characterizations of reflexive spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-440
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Strict feasibility of generalized complementarity problems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-20
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
The multidirectional mean value inequalities with second order information
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-172
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
The turnpike result for approximate solutions of nonautonomous variational problems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-130
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
Optimality criteria in set-valued optimization
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-232
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
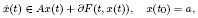
 ,
, 