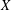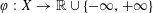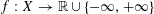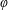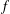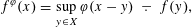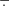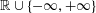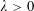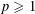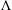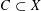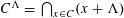Refine listing
Actions for selected content:
122 results in 49Jxx
Minimizing movements for oscillating energies: the critical regime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 719-737
- Print publication:
- June 2019
-
- Article
- Export citation
Existence of normalized solutions for nonlinear fractional Schrödinger equations with trapping potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 617-653
- Print publication:
- June 2019
-
- Article
- Export citation
Existence results for Kirchhoff–type superlinear problems involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1061-1081
- Print publication:
- August 2019
-
- Article
- Export citation
INFINITELY MANY SOLUTIONS FOR NONLOCAL SYSTEMS INVOLVING FRACTIONAL LAPLACIAN UNDER NONCOMPACT SETTINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 215-233
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Large data limit for a phase transition model with the p-Laplacian on point clouds
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 14 November 2018, pp. 185-231
-
- Article
- Export citation
A measure theoretic approach to traffic flow optimisation on networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 1187-1209
-
- Article
- Export citation
On the Mabinogion urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 327-346
- Print publication:
- June 2018
-
- Article
- Export citation
New relaxation theorems with applications to strong materials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 1029-1047
- Print publication:
- October 2018
-
- Article
- Export citation
A new analytical approach to consistency and overfitting in regularized empirical risk minimization
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 28 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 20 July 2017, pp. 886-921
-
- Article
-
- You have access
- Export citation
Spectral Method Approximation of Flow Optimal Control Problems with H 1-Norm State Constraint
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 614-638
- Print publication:
- August 2017
-
- Article
- Export citation
Convergence of a Time Discretization for a Nonlinear Second-Order Inclusion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 29 May 2017, pp. 93-120
-
- Article
- Export citation
Three periodic solutions for discontinuous perturbations of the vector p-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 673-681
- Print publication:
- August 2017
-
- Article
- Export citation
Curvature-dependent energies: a geometric and analytical approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 449-503
- Print publication:
- June 2017
-
- Article
- Export citation
Total Variation Based Parameter-Free Model for Impulse Noise Removal
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 186-204
- Print publication:
- February 2017
-
- Article
- Export citation
ENVELOPES FOR SETS AND FUNCTIONS: REGULARIZATION AND GENERALIZED CONJUGACY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 February 2017, pp. 383-432
- Print publication:
- 2017
-
- Article
- Export citation
GLOBAL ANALYSIS OF ONE-DIMENSIONAL VARIATIONAL PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 167-168
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Dynamics of screw dislocations: A generalised minimising-movements scheme approach†
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 28 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 03 November 2016, pp. 636-655
-
- Article
- Export citation
Error Estimates of Mixed Methods for Optimal Control Problems Governed by General Elliptic Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1050-1071
- Print publication:
- December 2016
-
- Article
- Export citation
MULTISYMPLECTIC VARIATIONAL INTEGRATORS FOR NONSMOOTH LAGRANGIAN CONTINUUM MECHANICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e19
-
- Article
-
- You have access
- Open access
- Export citation
METRIC REGULARITY—A SURVEY PART II. APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 376-417
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
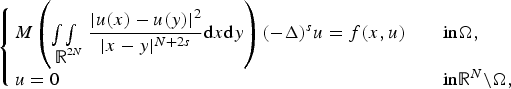
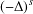
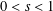
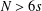
 .
.