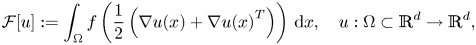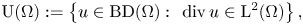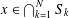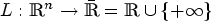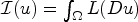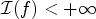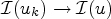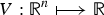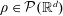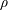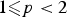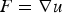Refine listing
Actions for selected content:
124 results in 49Jxx
Minimizing movements for forced anisotropic mean curvature flow of partitions with mobilities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 1135-1170
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
A dynamic thermo-mechanical actuator system with contact and Barber's heat exchange boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 May 2020, pp. 734-760
- Print publication:
- April 2021
-
- Article
- Export citation
Local minimizers in absence of ground states for the critical NLS energy on metric graphs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 May 2020, pp. 705-733
- Print publication:
- April 2021
-
- Article
- Export citation
Existence and multiplicity of solutions for discontinuous elliptic problems in ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 April 2020, pp. 548-572
- Print publication:
- April 2021
-
- Article
- Export citation
On the relaxation of integral functionals depending on the symmetrized gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 473-508
- Print publication:
- April 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation
ON THE REGULARITY OF SETS IN RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 386-405
- Print publication:
- June 2021
-
- Article
- Export citation
A new class of hyperbolic variational–hemivariational inequalities driven by non-linear evolution equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 59-88
-
- Article
-
- You have access
- Open access
- Export citation
SURVEY: SIXTY YEARS OF DOUGLAS–RACHFORD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 333-370
- Print publication:
- June 2021
-
- Article
- Export citation
Stable minimizers of functionals of the gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 05 July 2019, pp. 2642-2655
- Print publication:
- October 2020
-
- Article
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
On c-cyclical monotonicity for optimal transport problem with Coulomb cost
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 23 May 2019, pp. 1210-1219
-
- Article
- Export citation
A tale of two approaches to heteroclinic solutions for Φ-Laplacian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 May 2019, pp. 2535-2572
- Print publication:
- October 2020
-
- Article
- Export citation
Marginals with Finite Repulsive Cost
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 373-391
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF QUASICONVEX AND PSEUDOCONVEX FUNCTIONS BY THEIR SECOND-ORDER REGULAR SUBDIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 217-229
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Nonlinear systems coupled through multi-marginal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 April 2019, pp. 450-469
-
- Article
- Export citation
MONOTONE AND PSEUDO-MONOTONE EQUILIBRIUM PROBLEMS IN HADAMARD SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 March 2019, pp. 220-242
- Print publication:
- April 2021
-
- Article
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
Quantitative estimates for bending energies and applications to non-local variational problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 131-169
- Print publication:
- February 2020
-
- Article
- Export citation
Low Complexity Solutions of the Allen–Cahn Equation on Three-spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 287-291
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation