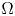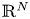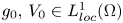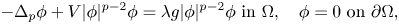Refine listing
Actions for selected content:
122 results in 49Jxx
A strongly convergent algorithm for solving multiple set split equality equilibrium and fixed point problems in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 475-515
-
- Article
- Export citation
Non-local approximation of free-discontinuity problems in linear elasticity and application to stochastic homogenisation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1060-1094
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extending linear growth functionals to functions of bounded fractional variation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 February 2023, pp. 304-327
- Print publication:
- February 2024
-
- Article
- Export citation
Optimal proportional reinsurance to maximize an insurer’s exponential utility under unobservable drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 21 February 2023, pp. 874-894
- Print publication:
- September 2023
-
- Article
- Export citation
Invariant ideals and their applications to the turnpike theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 959-975
- Print publication:
- September 2023
-
- Article
- Export citation
Pressure live loads and the variational derivation of linear elasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1929-1964
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the optimization of the first weighted eigenvalue
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1777-1804
- Print publication:
- December 2023
-
- Article
- Export citation
TRANSVERSALITY, REGULARITY AND ERROR BOUNDS IN VARIATIONAL ANALYSIS AND OPTIMISATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 167-169
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Relaxation for an optimal design problem in BD(Ω)
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 721-763
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Γ-convergence and stochastic homogenization of degenerate integral functionals in weighted Sobolev spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 491-544
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brittle fracture in linearly elastic plates
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 November 2021, pp. 68-103
- Print publication:
- February 2023
-
- Article
- Export citation
Unbalanced optimal total variation transport problems and generalized Wasserstein barycenters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 674-700
- Print publication:
- June 2022
-
- Article
- Export citation
Strong well-posedness and inverse identification problem of a non-local phase field tumour model with degenerate mobilities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 267-308
-
- Article
-
- You have access
- Open access
- Export citation
AN OPTIMAL LINEAR FILTER FOR ESTIMATION OF RANDOM FUNCTIONS IN HILBERT SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 07 January 2021, pp. 274-301
-
- Article
-
- You have access
- Export citation
Asymptotic variational analysis of incompressible elastic strings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 25 September 2020, pp. 1487-1514
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
On a family of torsional creep problems in Finsler metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 02 September 2020, pp. 24-41
- Print publication:
- February 2022
-
- Article
- Export citation
Continuous-domain assignment flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 01 September 2020, pp. 570-597
-
- Article
- Export citation
Minimizing movements for forced anisotropic mean curvature flow of partitions with mobilities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 1135-1170
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
A dynamic thermo-mechanical actuator system with contact and Barber's heat exchange boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 May 2020, pp. 734-760
- Print publication:
- April 2021
-
- Article
- Export citation