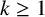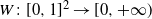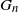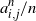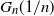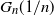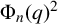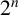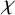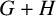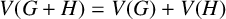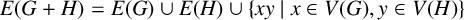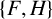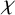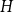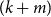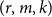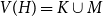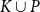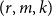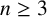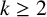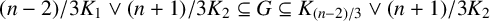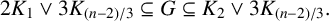Refine listing
Actions for selected content:
1716 results in 05xxx
ON A CONJECTURE REGARDING THE SYMMETRIC DIFFERENCE OF CERTAIN SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 397-404
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 October 2024, pp. 1-51
-
- Article
- Export citation
ON THE RAMSEY NUMBERS OF TREE GRAPHS VERSUS CERTAIN GENERALISED WHEEL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 08 October 2024, pp. 564-565
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
The k-core in percolated dense graph sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 298-318
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR SUMS OF MACMAHON’S q-CATALAN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 416-427
- Print publication:
- June 2025
-
- Article
- Export citation
A PROOF OF HIRSCHHORN’S CONJECTURE ON
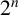 $2^n$-DISSECTION OF EULER’S PRODUCT
$2^n$-DISSECTION OF EULER’S PRODUCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 186-196
- Print publication:
- April 2025
-
- Article
- Export citation
The game of Cops and Robber on geodesic spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1827-1860
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1060-1084
-
- Article
- Export citation
REFERENCE DIGRAPHS OF NON-SELF-REFERENTIAL PARADOXES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 349-366
- Print publication:
- March 2025
-
- Article
- Export citation
A NOTE ON
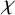 $\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
$\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 23-29
- Print publication:
- August 2025
-
- Article
- Export citation
The List-Ramsey threshold for families of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 829-851
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 795-806
-
- Article
- Export citation
SPECTRAL CLUSTERING AND LONG TIMESERIES CLASSIFICATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 121-131
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 742-768
-
- Article
- Export citation
List packing number of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 807-828
-
- Article
- Export citation
KRONECKER COEFFICIENTS FOR (DUAL) SYMMETRIC INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 65-90
- Print publication:
- February 2025
-
- Article
- Export citation
INEQUALITIES AND UNIFORM ASYMPTOTIC FORMULAE FOR SPT-CRANK OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 56-67
- Print publication:
- February 2025
-
- Article
- Export citation
EXTREMAL GRAPHS FOR DEGREE SUMS AND DOMINATING CYCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 205-211
- Print publication:
- April 2025
-
- Article
- Export citation
GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 197-204
- Print publication:
- April 2025
-
- Article
- Export citation
Quenched worst-case scenario for root deletion in targeted cutting of random recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 September 2024, pp. 67-83
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation