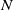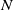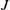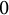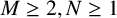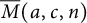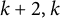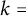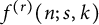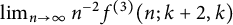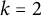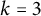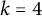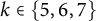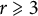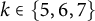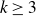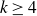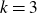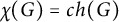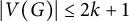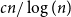Refine listing
Actions for selected content:
1716 results in 05xxx
DERIVATIVES OF THETA FUNCTIONS AS TRACES OF PARTITION EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 284-295
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Actions of nilpotent groups on nilpotent groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 16 January 2025, pp. 228-231
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oriented Temperley–Lieb algebras and combinatorial Kazhdan–Lusztig theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
0-Hecke modules, domino tableaux, and type-B quasisymmetric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BASE SHIFTING SEQUENCES AND THE PALINDROME PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 385-396
- Print publication:
- June 2025
-
- Article
- Export citation
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
Restricted sumsets in multiplicative subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics for crank of overpartitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-34
-
- Article
- Export citation
On the binomial transforms of Apéry-like sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 359-376
- Print publication:
- June 2025
-
- Article
- Export citation
On the (
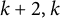 $k + \text{2}, k$)-problem of Brown, Erdős, and Sós for
$k + \text{2}, k$)-problem of Brown, Erdős, and Sós for 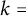 $k =$ 5,6,7
$k =$ 5,6,7
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dimension of the feasible region of pattern densities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-14
- Print publication:
- January 2025
-
- Article
- Export citation
Ramsey numbers of hypergraphs with a given size
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 31-44
- Print publication:
- January 2025
-
- Article
- Export citation
Minimum non-chromatic-choosable graphs with given chromatic number
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-32
-
- Article
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural convergence and algebraic roots
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 392-400
-
- Article
- Export citation
Vines and MAT-labeled graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 December 2024, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 220-226
- Print publication:
- October 2025
-
- Article
- Export citation
Essential covers of the hypercube require many hyperplanes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 16 December 2024, pp. 326-337
-
- Article
- Export citation
Tree universality in positional games
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 338-358
-
- Article
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation