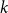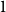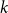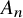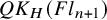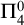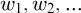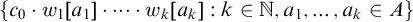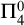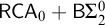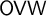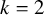Refine listing
Actions for selected content:
1716 results in 05xxx
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
ON NEW MINIMAL EXCLUDANTS OF OVERPARTITIONS RELATED TO SOME q-SERIES OF RAMANUJAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-13
- Print publication:
- August 2025
-
- Article
- Export citation
THE TREE PIGEONHOLE PRINCIPLE IN THE WEIHRAUCH DEGREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An efficient asymmetric removal lemma and its limitations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pebble trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite flags and Schubert polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measurable Vizing’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Face enumeration for split matroid polytopes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-544
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum bumpless pipe dreams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 February 2025, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Satisfiability thresholds for regular occupation problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 491-527
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete group actions on 3-manifolds and embeddable Cayley complexes
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
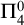 $\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
On perfect subdivision tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 421-444
-
- Article
- Export citation
Kostant’s problem for parabolic Verma modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 594-615
-
- Article
- Export citation
Bender–Knuth Billiards in Coxeter Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finding product sets in some classes of amenable groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypergraph independence polynomials with a zero close to the origin
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 486-490
-
- Article
- Export citation
Rigidity of symmetric simplicial complexes and the lower bound theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation