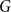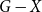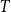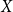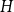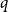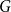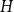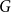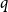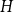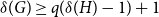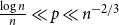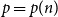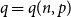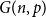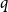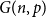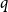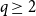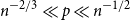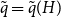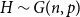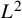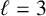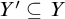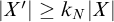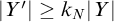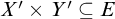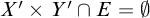Refine listing
Actions for selected content:
1717 results in 05xxx
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NUMERICAL SEMIGROUPS FROM RATIONAL MATRICES II: MATRICIAL DIMENSION DOES NOT EXCEED MULTIPLICITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 155-162
- Print publication:
- August 2025
-
- Article
- Export citation
Twin-width of sparse random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 401-420
-
- Article
- Export citation
Tight bound for the Erdős–Pósa property of tree minors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 321-325
-
- Article
- Export citation
The power of many colours
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average distance in a general class of scale-free networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 371-406
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuum limit for interacting systems on adaptive networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 December 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey simplicity of random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 298-320
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An inverse Grassmannian Littlewood–Richardson rule and extensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 December 2024, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NEIGHBOURHOODS IN THE ENHANCED POWER GRAPH ASSOCIATED WITH A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 149-154
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cubical setting for discrete homotopy theory, revisited
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 21 March 2025, pp. 2856-2903
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular Schur labeled skew shape posets and their 0-Hecke modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological structures of large-scale interacting systems via uniform functions and forms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING CONGRUENCES FOR OVERPARTITIONS WITH
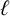 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 478-489
- Print publication:
- June 2025
-
- Article
- Export citation
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Long induced paths in expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 276-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noisy group testing via spatial coupling
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 210-258
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE STRONG ERDŐS–HAJNAL PROPERTY FOR GRAPHS WITH BOUNDED VC-MINIMAL COMPLEXITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
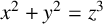 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation