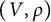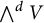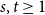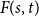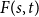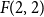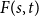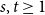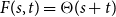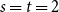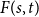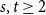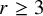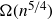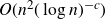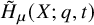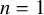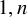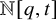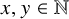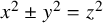Refine listing
Actions for selected content:
1716 results in 05xxx
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
AUTOMORPHISM GROUPS OF BICOSET DIGRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 30-46
- Print publication:
- August 2025
-
- Article
- Export citation
The real-time growth rate of stochastic epidemics on random intersection graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1132-1155
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on digraph splitting
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 559-564
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NEW TRUNCATED IDENTITIES AND PARTITION THEOREMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
- Export citation
The operad of Latin hypercubes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 475-486
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extremal, enumerative and probabilistic results on ordered hypergraph matchings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 March 2025, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A step towards a general density Corrádi–Hajnal theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Highly connected orientations from edge-disjoint rigid subgraphs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 March 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The asymptotics of the expected Betti numbers of preferential attachment clique complexes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 940-968
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite Hypergraph Families with Rich Extremal Turán Constructions via Mixing Patterns
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 March 2025, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
Common graphs with arbitrary chromatic number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 594-634
- Print publication:
- March 2025
-
- Article
- Export citation
LONGEST CYCLES AND LONGEST CHORDLESS CYCLES IN
 $2$-CONNECTED GRAPHS
$2$-CONNECTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 401-409
- Print publication:
- December 2025
-
- Article
- Export citation
Forman–Ricci communicability curvature of graphs and networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1096-1120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graph connectivity with fixed endpoints in the random-connection model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 370-396
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A raising operator formula for Macdonald polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal H-factors and covers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 136-152
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 505-508
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation