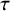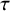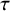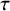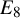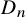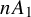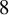Refine listing
Actions for selected content:
1713 results in 05xxx
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Ideals and their Fitting ideals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 30 July 2025, pp. 609-621
- Print publication:
- November 2025
-
- Article
- Export citation
ENUMERATION AND DIVISIBILITY OF HIGHER DIMENSIONAL KING WALKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-12
-
- Article
- Export citation
Posets arising from decompositions of objects in a monoidal category
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 July 2025, e123
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hook length inequalities for t-regular partitions in the t-aspect
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-12
-
- Article
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-22
-
- Article
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local generation of tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 18 July 2025, pp. 3377-3418
- Print publication:
- November 2025
-
- Article
- Export citation
Wreath Macdonald operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation graph of support
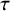 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ceresa period from tropical homology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-one dual characters of flagged Weyl modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-23
-
- Article
- Export citation
Orthogonal roots, Macdonald representations, and quasiparabolic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in structured graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. 625-634
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THREE ALGORITHMIC APPROACHES TO THE GENERAL POSITION PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-9
-
- Article
- Export citation
NONASSORTATIVE COMMUNITY STRUCTURES IN COMPLEX NETWORKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 04 July 2025, pp. 561-562
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
Schubert polynomial expansions revisited
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 July 2025, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large deviation principle for block models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 680-753
-
- Article
- Export citation
Common pairs of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 649-670
-
- Article
- Export citation
K-Orbit closures and Hessenberg varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 June 2025, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation