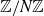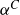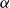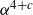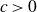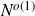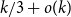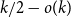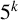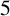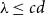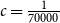Refine listing
Actions for selected content:
1716 results in 05xxx
Short proof of the hypergraph container theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 621-624
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation
Large cuts in hypergraphs via energy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 45-61
- Print publication:
- July 2025
-
- Article
- Export citation
A REMARK ON GENERALISED CUBIC PARTITIONS MODULO
 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 May 2025, pp. 1-5
-
- Article
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shuffle formula in science fiction for Macdonald polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1075-1127
- Print publication:
- May 2025
-
- Article
- Export citation
Hypergraph removal with polynomial bounds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 321-330
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colouring random subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 585-595
-
- Article
- Export citation
Cycle Partitions in Dense Regular Digraphs and Oriented Graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kohayakawa–Kreuter conjecture
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 293-320
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Ramsey–Turán density for cliques
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 April 2025, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VERY SHORT PROOF OF SIDORENKO’S INEQUALITY FOR COUNTS OF HOMOMORPHISMS BETWEEN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
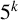 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 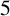 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 449-457
- Print publication:
- December 2025
-
- Article
- Export citation
COMBINATORIAL PROOFS FOR TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-5
-
- Article
- Export citation
Length spectrum of large genus random metric maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 April 2025, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COLORING EQUILATERAL TRIANGLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-14
-
- Article
- Export citation
Newton–Maclaurin type inequalities for linear combinations of elementary symmetric functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-18
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hamiltonicity of sparse pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 596-620
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric multiple zeta functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation