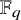Refine listing
Actions for selected content:
1717 results in 05xxx
Delta and Theta Operator Expansions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 March 2024, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
- Export citation
Antidirected subgraphs of oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IDEMPOTENT GENERATORS OF INCIDENCE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 488-497
- Print publication:
- December 2024
-
- Article
- Export citation
Perfect sampling of stochastic matching models with reneging
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1307-1339
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
GENERATING FUNCTIONS FOR THE QUOTIENTS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 427-438
- Print publication:
- December 2024
-
- Article
- Export citation
Average Jaccard index of random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1139-1152
- Print publication:
- December 2024
-
- Article
- Export citation
Connectivity of random graphs after centrality-based vertex removal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 967-998
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-Point Concentration of the Independence Number of the Random Graph
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 February 2024, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 411-431
-
- Article
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
EDGE WEIGHTING FUNCTIONS ON THE SEMITOTAL DOMINATING SET OF CLAW-FREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 177-188
- Print publication:
- October 2024
-
- Article
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Network-based kinetic models: Emergence of a statistical description of the graph topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Electrical networks and the grove algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 01 February 2024, pp. 631-664
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Δ–Springer varieties and Hall–Littlewood polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
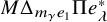
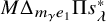
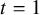
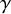
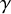
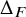
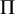
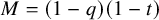
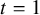
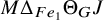
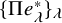

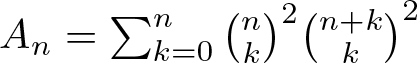

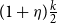
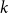
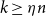
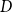



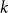
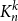
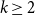
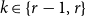
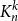
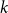

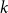
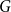

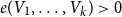
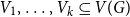
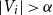
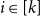




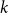
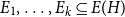
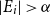
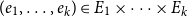

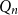
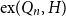
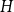
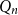
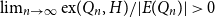
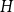
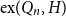
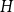
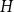







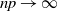
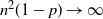

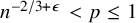
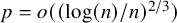
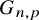

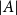
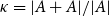

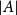
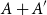
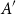
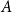

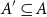

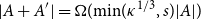

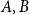
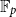
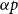
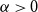
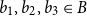
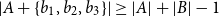
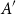
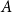
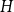
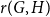
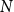
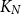
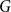
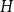
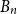

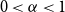
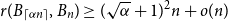
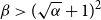
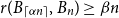

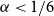
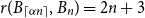

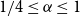
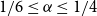

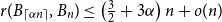
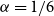
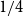
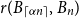
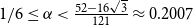
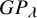
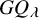
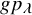
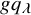
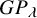
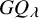
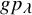
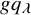
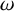
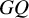
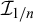
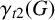
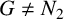
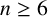
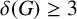
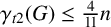
 .
.