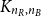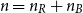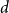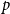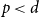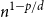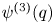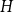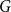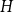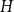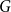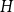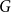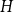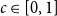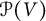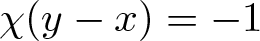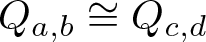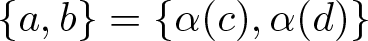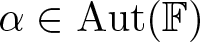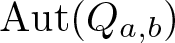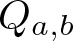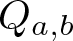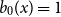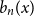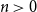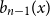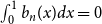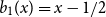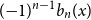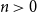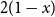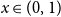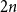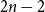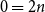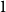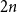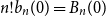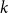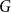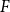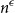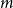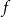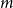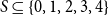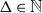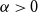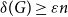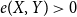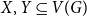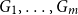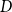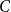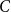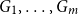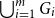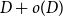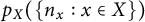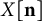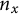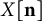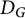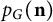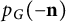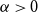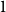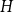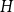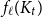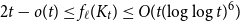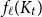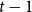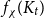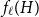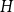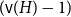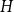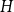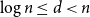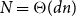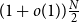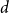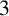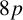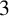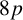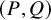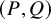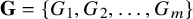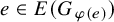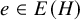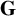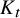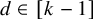Refine listing
Actions for selected content:
1717 results in 05xxx
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation
Local convergence of critical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 851-857
- Print publication:
- September 2024
-
- Article
- Export citation
Threshold graphs maximise homomorphism densities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 300-318
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graphical methods and rings of invariants on the symmetric algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2173-2198
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros, chaotic ratios and the computational complexity of approximating the independence polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 459-494
- Print publication:
- March 2024
-
- Article
- Export citation
Isomorphisms of quadratic quasigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 24 November 2023, pp. 1085-1109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 210-237
-
- Article
- Export citation
Large cliques or cocliques in hypergraphs with forbidden order-size pairs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 286-299
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spanning trees in graphs without large bipartite holes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 270-285
-
- Article
-
- You have access
- HTML
- Export citation
A special case of Vu’s conjecture: colouring nearly disjoint graphs of bounded maximum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 179-195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 2073-2114
- Print publication:
- December 2024
-
- Article
- Export citation
On oriented cycles in randomly perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 157-178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the choosability of
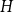 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Burstein’s permutation conjecture, Hong and Li’s inversion sequence conjecture and restricted Eulerian distributions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1179-1201
-
- Article
- Export citation
Spanning subdivisions in Dirac graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 121-128
-
- Article
- Export citation
NOWHERE-ZERO
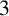 $3$-FLOWS IN CAYLEY GRAPHS OF ORDER
$3$-FLOWS IN CAYLEY GRAPHS OF ORDER 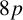 $8p$
$8p$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1-11
- Print publication:
- August 2024
-
- Article
- Export citation
Skew RSK dynamics: Greene invariants, affine crystals and applications to q-Whittaker polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 October 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rainbow spanning structures in graph and hypergraph systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 October 2023, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINATORIAL BOUNDS IN DISTAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 October 2023, pp. 1-33
-
- Article
- Export citation