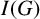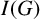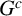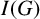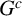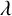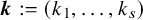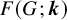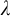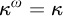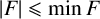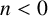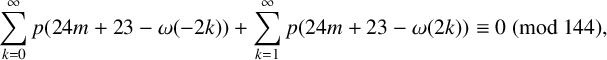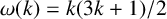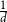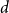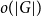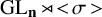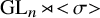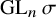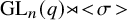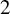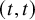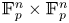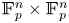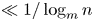Refine listing
Actions for selected content:
1717 results in 05xxx
CONGRUENCES FOR RANKS OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 280-290
- Print publication:
- October 2024
-
- Article
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
- Export citation
A Pipe Dream Perspective on Totally Symmetric Self-Complementary Plane Partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1798-1816
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration of measure for graphon particle system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1279-1306
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local weak limit of preferential attachment random trees with additive fitness
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 785-824
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The location of high-degree vertices in weighted recursive graphs with bounded random weights
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 868-926
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact solutions to the Erdős-Rothschild problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARTITION OF LARGE SUBSETS OF SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-6
-
- Article
- Export citation
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 19-31
- Print publication:
- August 2024
-
- Article
- Export citation
DIVISIBILITY OF SUMS OF PARTITION NUMBERS BY MULTIPLES OF 2 AND 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 271-279
- Print publication:
- October 2024
-
- Article
- Export citation
Percolation on irregular high-dimensional product graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 377-403
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
E-Polynomials of Generic
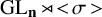 $\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
$\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
- Export citation
Unified bounds for the independence number of graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 97-117
- Print publication:
- February 2025
-
- Article
- Export citation
Product structure of graph classes with bounded treewidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 December 2023, pp. 351-376
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A question of Frohardt on
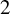 $2$-groups, skew translation quadrangles of even order and cyclic STGQs
$2$-groups, skew translation quadrangles of even order and cyclic STGQs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsets of
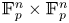 $\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 176-236
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation