A recent result of Eisenbud–Schreyer and Boij–Söderberg proves that the Betti diagram of any graded module decomposes as a positive rational linear combination of pure diagrams. When does this numerical decomposition correspond to an actual filtration of the minimal free resolution? Our main result gives a sufficient condition for this to happen. We apply it to show the non-existence of free resolutions with some plausible-looking Betti diagrams and to study the semigroup of quiver representations of the simplest ‘wild’ quiver.

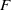For a characteristic-$p\gt 0$ variety $X$ with controlled $F$-singularities, we state conditions which imply that a divisorial sheaf is Cohen–Macaulay or at least has depth $\geq $3 at certain points. This mirrors results of Kollár for varieties in characteristic 0. As an application, we show that relative canonical sheaves are compatible with arbitrary base change for certain families with sharply $F$-pure fibers.

In a recent paper, Iyama and Yoshino considered two interesting examples of isolated singularities over which it is possible to classify the indecomposable maximal Cohen–Macaulay modules in terms of linear algebra data. In this paper, we present two new approaches to these examples. In the first approach we give a relation with cluster categories. In the second approach we use Orlov’s result on the graded singularity category.

This paper takes a new look at ideals generated by 2×2 minors of 2×3 matrices whose entries are powers of three elements not necessarily forming a regular sequence. A special case of this is the ideals determining monomial curves in three-dimensional space, which were studied by Herzog. In the broader context studied here, these ideals are identified as Northcott ideals in the sense of Vasconcelos, and so their liaison properties are displayed. It is shown that they are set-theoretically complete intersections, revisiting the work of Bresinsky and of Valla. Even when the three elements are taken to be variables in a polynomial ring in three variables over a field, this point of view gives a larger class of ideals than just the defining ideals of monomial curves. We then characterize when the ideals in this larger class are prime, we show that they are usually radical and, using the theory of multiplicities, we give upper bounds on the number of their minimal prime ideals, one of these primes being a uniquely determined prime ideal of definition of a monomial curve. Finally, we provide examples of characteristic-dependent minimal prime and primary structures for these ideals.

In this paper we prove that a generalized version of the Minimal Resolution Conjecture given by Mustaţă holds for certain general sets of points on a smooth cubic surface $X\,\subset \,{{\mathbb{P}}^{3}}$. The main tool used is Gorenstein liaison theory and, more precisely, the relationship between the free resolutions of two linked schemes.

Let R and S be commutative rings, not necessarily with identity. We investigate the ideals, prime ideals, radical ideals, primary ideals, and maximal ideals of R×S. Unlike the case where R and S have an identity, an ideal (or primary ideal, or maximal ideal) of R×S need not be a ‘subproduct’ I×J of ideals. 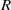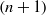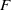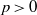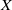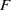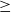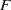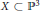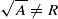We show that for a ring R, for each commutative ring S every ideal (or primary ideal, or maximal ideal) is a subproduct if and only if R is an e-ring (that is, for r∈R, there exists er∈R with err=r) (or u-ring (that is, for each proper ideal A of R, )), the Abelian group (R/R2 ,+)has no maximal subgroups).

We generalize Gaeta’s theorem to the family of determinantal schemes. In other words, we show that the schemes defined by minors of a fixed size of a matrix with polynomial entries belong to the same G-biliaison class of a complete intersection whenever they have maximal possible codimension, given the size of the matrix and of the minors that define them.

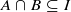A proper ideal I of a ring R is said to be strongly irreducible if for each pair of ideals A and B of R, implies that eithe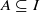r or 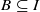. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.

In what follows, R will denote a commutative domain with 1, and Q(≠R) its field of quotients, which is viewed here as an R-module. By RP we denote the localization of R at the maximal ideal P, and more generally, by MP = Rp⊗RM the localization of the R-module M at P, which we define to be the P-component of M. The symbol R* will mean the multiplicative monoid of nonzero elements of R. For a submonoid S of R*, Rs will denote the localization of R at S.

Filters and אּ-complete filters can be used to produce set-theoretic extensions of direct sums and direct products. They can be applied to generalize theorems in module theory which involve these. For example, the theorem, stating that a ring is noetherian, if, and only if, direct sums of injectives are injective, can be generalized, provided we replace noetherian by Xa-noetherian and direct sums by אּ- complete filter sums with a suitable property.

A module M over a ring R is κ-projective, κ a cardinal, if M is projective relative to all exact sequence of R-modules 0 → A → B → C → 0 such that C has a generating set of cardinality less than κ. A structure theorem for κ-projective modules over Dedekind domains is proven, and the κ-projectivity of M is related to properties of ExtR (M, ⊕ R). Using results of S. Chase, S. Shelah and P. Eklof, the existence of non-projective и1-projective modules is shown to undecidable, while both the Continuum Hypothesis and its denial (Plus Martin's Axiom) imply the existence of a reduced И0-projective Z-module which is not free.

Let N be a direct summand of a module which is a direct sum of modules of torsion-free rank one over a discrete valuation ring. Then there is a torsion module T such that N⊕T is also a direct sum of modules of torsion-free rank one.

Let R be a commutative ring with identity, and let U be a unitary commutative R-algebra with identity. In [1] Gilmer defines the (l/n)th power (n a positive integer) of a valuation ideal R when R is a domain. Sections 2, 3 of the present note are devoted to the study of an extension of this notion to positive rational powers of an arbitrary R-submodule of U.