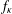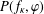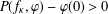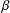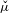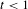Refine listing
Actions for selected content:
258 results in 37Dxx
Examples of exponentially many collisions in a hard ball system
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2754-2769
- Print publication:
- September 2021
-
- Article
- Export citation
Classification of partially hyperbolic diffeomorphisms under some rigid conditions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 2770-2781
- Print publication:
- September 2021
-
- Article
- Export citation
Large deviations and central limit theorems for sequential and random systems of intermittent maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 2805-2832
- Print publication:
- September 2021
-
- Article
- Export citation
The conformal measures of a normal subgroup of a cocompact Fuchsian group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2845-2878
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Cohomology of fiber-bunched twisted cocycles over hyperbolic systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 844-860
-
- Article
- Export citation
STOCHASTIC POTENTIALS OF INTERMITTENT MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 145-153
- Print publication:
- February 2021
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
Approximating integrals with respect to stationary probability measures of iterated function systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2294-2310
- Print publication:
- August 2021
-
- Article
- Export citation
Primitive rational points on expanding horocycles in products of the modular surface with the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1706-1750
- Print publication:
- June 2021
-
- Article
- Export citation
Extensions with shrinking fibers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 1795-1834
- Print publication:
- June 2021
-
- Article
- Export citation
Thermodynamic formalism for Haar systems in noncommutative integration: transverse functions and entropy of transverse measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 27 March 2020, pp. 1835-1863
- Print publication:
- June 2021
-
- Article
- Export citation
Unique equilibrium states, large deviations and Lyapunov spectra for the Katok map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 20 March 2020, pp. 2182-2219
- Print publication:
- July 2021
-
- Article
- Export citation
Asymptotic escape rates and limiting distributions for multimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 1656-1705
- Print publication:
- June 2021
-
- Article
- Export citation
A solution to Flinn’s conjecture on weakly expansive flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 1390-1396
- Print publication:
- May 2021
-
- Article
- Export citation
Attractors associated to a family of hyperbolic
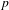 $p$ -adic plane automorphisms
$p$ -adic plane automorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1867-1882
- Print publication:
- June 2021
-
- Article
- Export citation
Statistical properties for compositions of standard maps with increasing coefficient
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 981-1024
- Print publication:
- April 2021
-
- Article
- Export citation
On preimage entropy, folding entropy and stable entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1217-1249
- Print publication:
- April 2021
-
- Article
- Export citation
An example of a planar Anosov diffeomorphism without fixed points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 923-934
- Print publication:
- March 2021
-
- Article
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
Anosov diffeomorphisms of products I. Negative curvature and rational homology spheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 553-569
- Print publication:
- February 2021
-
- Article
- Export citation