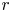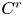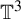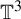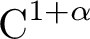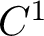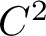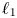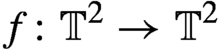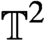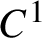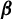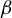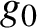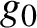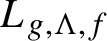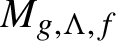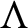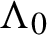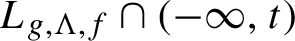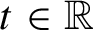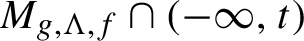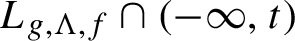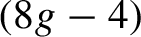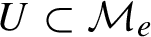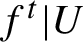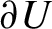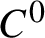Refine listing
Actions for selected content:
258 results in 37Dxx
Gaps of saddle connection directions for some branched covers of tori
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 August 2021, pp. 3191-3245
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fast growth of the number of periodic points arising from heterodimensional connections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1899-1963
- Print publication:
- September 2021
-
- Article
- Export citation
Centralizers of derived-from-Anosov systems on
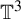 ${\mathbb T}^3$: rigidity versus triviality
${\mathbb T}^3$: rigidity versus triviality
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2841-2865
- Print publication:
- September 2022
-
- Article
- Export citation
GEOMETRICAL AND MEASURE-THEORETIC STRUCTURES OF MAPS WITH A MOSTLY EXPANDING CENTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 919-959
- Print publication:
- March 2023
-
- Article
- Export citation
A new proof of the dimension gap for the Gauss map
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 43-71
- Print publication:
- January 2022
-
- Article
- Export citation
Homology and K-theory of dynamical systems I. Torsion-free ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2630-2660
- Print publication:
- August 2022
-
- Article
- Export citation
Anosov diffeomorphisms, anisotropic BV spaces and regularity of foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2431-2467
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
Flexibility of Lyapunov exponents with respect to two classes of measures on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 737-776
- Print publication:
- February 2022
-
- Article
- Export citation
Absolute continuity, Lyapunov exponents, and rigidity II: systems with compact center leaves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 437-490
- Print publication:
- February 2022
-
- Article
- Export citation
Thermodynamics of smooth models of pseudo–Anosov homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 1284-1326
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
Accessibility and centralizers for partially hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 835-854
- Print publication:
- March 2022
-
- Article
- Export citation
Equilibrium measures of the natural extension of
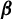 $\boldsymbol{\beta}$-shifts
$\boldsymbol{\beta}$-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2415-2430
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Ahlfors regularity and fractal dimension of Smale spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 29 April 2021, pp. 2281-2332
- Print publication:
- July 2022
-
- Article
- Export citation
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
- Print publication:
- June 2022
-
- Article
- Export citation
Central limit theorem of Brownian motions in pinched negative curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 2352-2381
- Print publication:
- July 2022
-
- Article
- Export citation
Margulis–Ruelle inequality for general manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 2064-2079
- Print publication:
- June 2022
-
- Article
- Export citation
Flexibility of measure-theoretic entropy of boundary maps associated to Fuchsian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 389-401
- Print publication:
- February 2022
-
- Article
- Export citation
The essential coexistence phenomenon in Hamiltonian dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 592-613
- Print publication:
- February 2022
-
- Article
- Export citation
Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2009-2027
- Print publication:
- June 2022
-
- Article
- Export citation