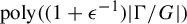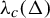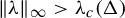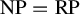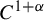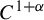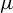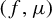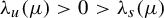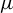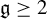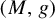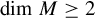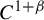Refine listing
Actions for selected content:
258 results in 37Dxx
A spectral approach to quenched linear and higher-order response for partially hyperbolic dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1026-1057
- Print publication:
- April 2024
-
- Article
- Export citation
A note on preimage entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 1468-1472
- Print publication:
- May 2024
-
- Article
- Export citation
Wasserstein convergence rates in the invariance principle for deterministic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1172-1191
- Print publication:
- April 2024
-
- Article
- Export citation
EQUILIBRIUM STATES FOR CENTER ISOMETRIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 02 June 2023, pp. 1295-1355
- Print publication:
- May 2024
-
- Article
- Export citation
Cancellations of periodic orbits for non-singular Morse–Smale flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 25 May 2023, pp. 1123-1171
- Print publication:
- April 2024
-
- Article
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Binary factors of shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 888-932
- Print publication:
- March 2024
-
- Article
- Export citation
On bifurcation of statistical properties of partially hyperbolic endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-944
- Print publication:
- March 2024
-
- Article
- Export citation
Dimension approximation in smooth dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 383-407
- Print publication:
- February 2024
-
- Article
- Export citation
Synchronization of coupled map lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 March 2023, pp. 143-163
-
- Article
- Export citation
A note on the differentiability of discrete Palmer's linearization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 22 March 2023, pp. 600-628
- Print publication:
- April 2024
-
- Article
- Export citation
Measures of maximal and full dimension for smooth maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 31-49
- Print publication:
- January 2024
-
- Article
- Export citation
Horseshoes and Lyapunov exponents for Banach cocycles over non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 674-704
- Print publication:
- February 2024
-
- Article
- Export citation
Thermodynamical u-formalism I: measures of maximal u-entropy for maps that factor over Anosov
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 290-333
- Print publication:
- January 2024
-
- Article
- Export citation
Construction and applications of proximal maps for typical cocycles
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 204-235
- Print publication:
- January 2024
-
- Article
- Export citation
Structural stability for fibrewise Anosov diffeomorphisms on principal torus bundles
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 February 2023, pp. 334-352
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sensitivity and historic behavior for continuous maps on Baire metric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 February 2023, pp. 1-30
- Print publication:
- January 2024
-
- Article
- Export citation
On the ergodicity of geodesic flows on surfaces without focal points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 4226-4248
- Print publication:
- December 2023
-
- Article
- Export citation
Invariant family of leaf measures and the Ledrappier–Young property for hyperbolic equilibrium states
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 3603-3635
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolicity and abundance of elliptical islands in annular billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 3545-3577
- Print publication:
- November 2023
-
- Article
- Export citation