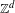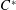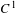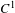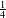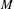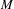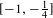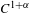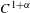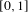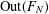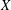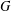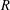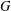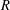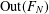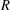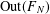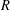Refine listing
Actions for selected content:
258 results in 37Dxx
Persistent Hall rays for Lagrange spectra at cusps of Riemann surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 2017-2072
- Print publication:
- August 2020
-
- Article
- Export citation
ON GENERATORS AND DISTURBANCES OF DYNAMICAL SYSTEMS IN THE CONTEXT OF CHAOTIC POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 76-85
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
On–off intermittency and chaotic walks
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1805-1842
- Print publication:
- July 2020
-
- Article
-
- You have access
- Open access
- Export citation
Potential kernel, hitting probabilities and distributional asymptotics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1894-1967
- Print publication:
- July 2020
-
- Article
- Export citation
Asymptotic Continuous Orbit Equivalence of Smale Spaces and Ruelle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1243-1296
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
NON-HYPERBOLIC ERGODIC MEASURES AND HORSESHOES IN PARTIALLY HYPERBOLIC HOMOCLINIC CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1765-1792
- Print publication:
- September 2020
-
- Article
- Export citation
Higher rank rigidity for Berwald spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 December 2018, pp. 1991-2016
- Print publication:
- July 2020
-
- Article
- Export citation
Manhattan curves for hyperbolic surfaces with cusps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1843-1874
- Print publication:
- July 2020
-
- Article
- Export citation
SPECTRAL ANALYSIS OF MORSE–SMALE FLOWS I: CONSTRUCTION OF THE ANISOTROPIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1409-1465
- Print publication:
- September 2020
-
- Article
- Export citation
Unique ergodicity of the horocycle flow on Riemannnian foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1459-1479
- Print publication:
- June 2020
-
- Article
- Export citation
The
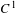 $C^{1}$ property of convex carrying simplices for competitive maps
$C^{1}$ property of convex carrying simplices for competitive maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1335-1350
- Print publication:
- May 2020
-
- Article
- Export citation
SRB measures for partially hyperbolic attractors of local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1545-1593
- Print publication:
- June 2020
-
- Article
- Export citation
Hyperbolic rank rigidity for manifolds of
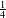 $\frac{1}{4}$-pinched negative curvature
$\frac{1}{4}$-pinched negative curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1194-1216
- Print publication:
- May 2020
-
- Article
- Export citation
On the stable ergodicity of Berger–Carrasco’s example
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1008-1056
- Print publication:
- April 2020
-
- Article
- Export citation
Simultaneous dense and non-dense orbits for certain partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 04 September 2018, pp. 1083-1107
- Print publication:
- April 2020
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
Explicit coupling argument for non-uniformly hyperbolic transformations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 06 July 2018, pp. 101-130
- Print publication:
- February 2019
-
- Article
- Export citation
On concentration properties of partially observed chaotic systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 440-479
- Print publication:
- June 2018
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
- Print publication:
- January 2020
-
- Article
- Export citation
COUNTING CONJUGACY CLASSES IN
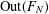 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 412-421
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation