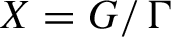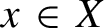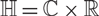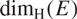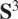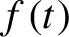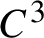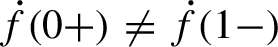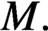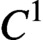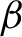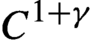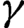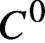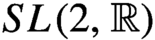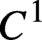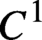Refine listing
Actions for selected content:
258 results in 37Dxx
There are no deviations for the ergodic averages of Giulietti–Liverani horocycle flows on the two-torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 500-513
- Print publication:
- February 2022
-
- Article
- Export citation
Non-dense orbits on homogeneous spaces and applications to geometry and number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1327-1372
- Print publication:
- April 2022
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
A piecewise smooth Fermi–Ulam pingpong with potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1847-1870
- Print publication:
- May 2022
-
- Article
- Export citation
Vortices over Riemann surfaces and dominated splittings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1781-1806
- Print publication:
- May 2022
-
- Article
- Export citation
CHAIN COMPONENTS WITH THE STABLE SHADOWING PROPERTY FOR C1 VECTOR FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 243-259
- Print publication:
- April 2021
-
- Article
- Export citation
A variational principle for the metric mean dimension of free semigroup actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 February 2021, pp. 65-85
- Print publication:
- January 2022
-
- Article
- Export citation
On subshifts with slow forbidden word growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 1487-1516
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
Diffeomorphism cocycles over partially hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 263-286
- Print publication:
- January 2022
-
- Article
- Export citation
Symbolic dynamics for non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2591-2658
- Print publication:
- September 2021
-
- Article
- Export citation
Continuity of Lyapunov exponents for non-uniformly fiber-bunched cocycles
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 3740-3767
- Print publication:
- December 2021
-
- Article
- Export citation
The set of points with Markovian symbolic dynamics for non-uniformly hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3244-3269
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Dynamical incoherence for a large class of partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3227-3243
- Print publication:
- November 2021
-
- Article
- Export citation
Unstable pressure and u-equilibrium states for partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3336-3362
- Print publication:
- November 2021
-
- Article
- Export citation
A strongly irreducible affine iterated function system with two invariant measures of maximal dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3417-3438
- Print publication:
- November 2021
-
- Article
- Export citation
Topological flows for hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3474-3520
- Print publication:
- November 2021
-
- Article
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Foliations and conjugacy, II: the Mendes conjecture for time-one maps of flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3307-3324
- Print publication:
- November 2021
-
- Article
- Export citation
Finitely many physical measures for sectional-hyperbolic attracting sets and statistical stability
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 2706-2733
- Print publication:
- September 2021
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation