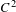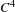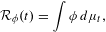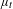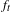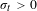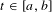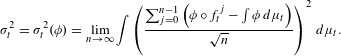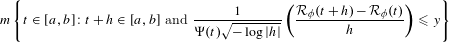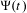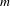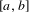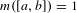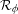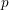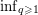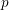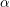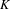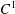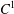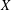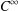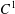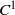Refine listing
Actions for selected content:
258 results in 37Dxx
Pair correlation for quadratic polynomials mod 1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 960-983
- Print publication:
- May 2018
-
- Article
- Export citation
Algebraic Limit Cycles on Quadratic Polynomial Differential Systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 27 February 2018, pp. 499-512
-
- Article
- Export citation
CENTRAL LIMIT THEOREM FOR THE MODULUS OF CONTINUITY OF AVERAGES OF OBSERVABLES ON TRANSVERSAL FAMILIES OF PIECEWISE EXPANDING UNIMODAL MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 673-733
- Print publication:
- June 2018
-
- Article
- Export citation
A version of a theorem of Pliss for non-uniform and non-invertible dichotomies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 225-243
- Print publication:
- April 2017
-
- Article
- Export citation
PERTURBATION OF THE SEMICLASSICAL SCHRÖDINGER EQUATION ON NEGATIVELY CURVED SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 27 August 2015, pp. 787-835
- Print publication:
- September 2017
-
- Article
- Export citation
DIMENSIONAL CHARACTERISTICS OF THE NONWANDERING SETS OF OPEN BILLIARDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 11 August 2015, pp. 511-513
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
NONUNIFORM EXPONENTIAL BEHAVIOUR AND TOPOLOGICAL EQUIVALENCE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 279-291
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
On the complexity of a putative counterexample to the
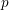 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1647-1662
- Print publication:
- September 2015
-
- Article
- Export citation
CENTER MANIFOLDS FOR PARTIALLY HYPERBOLIC SETS WITHOUT STRONG UNSTABLE CONNECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 11 March 2015, pp. 785-828
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
HYPERBOLICITY OF HOMOCLINIC CLASSES OF
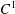 $C^{1}$ VECTOR FIELDS
$C^{1}$ VECTOR FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 375-389
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Knots which behave like the prime numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1235-1244
- Print publication:
- August 2013
-
- Article
- Export citation
A robustly chain transitive attractor with singularities of different indices
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 449-501
- Print publication:
- July 2013
-
- Article
- Export citation
Conjugacies for impulsive equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 65-78
-
- Article
-
- You have access
- Export citation
Scarring for quantum maps with simple spectrum
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1608-1612
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Pairs of periodic orbits with fixed homology difference
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 799-808
-
- Article
-
- You have access
- Export citation
C1-generic symplectic diffeomorphisms: partial hyperbolicity and zero centre Lyapunov exponents
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 26 March 2009, pp. 49-93
- Print publication:
- January 2010
-
- Article
- Export citation
AMBIGUITY IN THE DETERMINATION OF THE FREE ENERGY ASSOCIATED WITH THE CRITICAL CIRCLE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-184
-
- Article
-
- You have access
- Export citation
AN ALMOST EVERYWHERE VERSION OF SMÍTAL’S ORDER–CHAOS DICHOTOMY FOR INTERVAL MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 29-50
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation