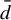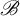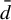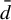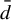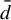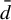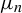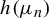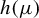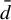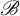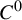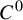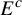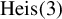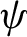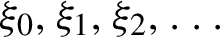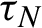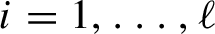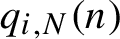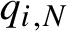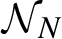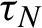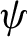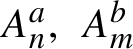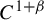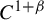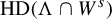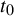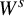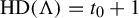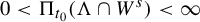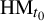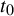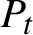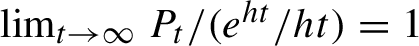Refine listing
Actions for selected content:
258 results in 37Dxx
On
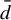 ${\bar d}$-approachability, entropy density and
${\bar d}$-approachability, entropy density and 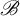 $\mathscr {B}$-free shifts
$\mathscr {B}$-free shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 943-970
- Print publication:
- March 2023
-
- Article
- Export citation
New approach to weighted topological entropy and pressure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 1004-1034
- Print publication:
- March 2023
-
- Article
- Export citation
Distribution in the unit tangent bundle of the geodesics of given type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 24 January 2022, pp. 887-903
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Carnot metrics, dynamics and local rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 614-664
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the equidistribution of unstable curves for pseudo-Anosov diffeomorphisms of compact surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 855-880
- Print publication:
- March 2022
-
- Article
- Export citation
Statistical stability and linear response for random hyperbolic dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 07 December 2021, pp. 515-544
- Print publication:
- February 2023
-
- Article
- Export citation
On
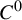 $C^0$-genericity of distributional chaos
$C^0$-genericity of distributional chaos
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 615-645
- Print publication:
- February 2023
-
- Article
- Export citation
Excursions to the cusps for geometrically finite hyperbolic orbifolds and equidistribution of closed geodesics in regular covers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 3745-3791
- Print publication:
- December 2022
-
- Article
- Export citation
Invariant measures for interval maps without Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 663-691
- Print publication:
- February 2023
-
- Article
- Export citation
Partially hyperbolic diffeomorphisms and Lagrangian contact structures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2583-2629
- Print publication:
- August 2022
-
- Article
- Export citation
The K-property for some unique equilibrium states in flows and homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2509-2532
- Print publication:
- August 2022
-
- Article
- Export citation
Limit theorems for numbers of multiple returns in non-conventional arrays
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1098-1121
- Print publication:
- March 2022
-
- Article
- Export citation
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
Equidistribution of horospheres in non-positive curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 28 October 2021, pp. 460-479
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flexibility of Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 554-591
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smoothness of stable holonomies inside center-stable manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3593-3618
- Print publication:
- December 2022
-
- Article
- Export citation
Hausdorff and packing dimensions and measures for nonlinear transversally non-conformal thin solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3458-3489
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting closed geodesics in a compact rank-one locally CAT(0) space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 August 2021, pp. 1220-1251
- Print publication:
- March 2022
-
- Article
- Export citation
Geodesic stretch, pressure metric and marked length spectrum rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 974-1022
- Print publication:
- March 2022
-
- Article
- Export citation
Transversal local rigidity of discrete abelian actions on Heisenberg nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 04 August 2021, pp. 3111-3151
- Print publication:
- October 2022
-
- Article
- Export citation