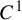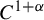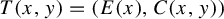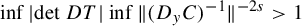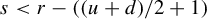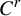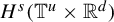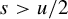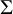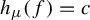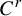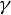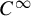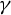Refine listing
Actions for selected content:
258 results in 37Dxx
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 216-233
- Print publication:
- October 2024
-
- Article
- Export citation
Upper, down, two-sided Lorenz attractor, collisions, merging, and switching
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 2737-2781
- Print publication:
- October 2024
-
- Article
- Export citation
Dimension estimates and approximation in non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 2975-3001
- Print publication:
- October 2024
-
- Article
- Export citation
Regularity and linear response formula of the SRB measures for solenoidal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 February 2024, pp. 2782-2831
- Print publication:
- October 2024
-
- Article
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 85-104
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting geodesics of given commutator length
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 December 2023, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium states for non-uniformly expanding skew products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2599-2620
- Print publication:
- September 2024
-
- Article
- Export citation
Constructing Birkhoff sections for pseudo-Anosov flows with controlled complexity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 2308-2360
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 2257-2288
- Print publication:
- August 2024
-
- Article
- Export citation
Smooth models for certain fibered partially hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2173-2198
- Print publication:
- August 2024
-
- Article
- Export citation
A mechanism for ejecting a horseshoe from a partially hyperbolic chain recurrence class
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 2080-2142
- Print publication:
- August 2024
-
- Article
- Export citation
Statistical determinism in non-Lipschitz dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1856-1884
- Print publication:
- July 2024
-
- Article
- Export citation
 $C^r$-chain closing lemma for certain partially hyperbolic diffeomorphisms
$C^r$-chain closing lemma for certain partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1923-1944
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Nonchaotic N-expansive homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1-9
- Print publication:
- February 2025
-
- Article
- Export citation
Conditional mixing in deterministic chaos
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1693-1723
- Print publication:
- June 2024
-
- Article
- Export citation
Uniform spectral gap and orthogeodesic counting for strong convergence of Kleinian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 August 2023, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On infinitely many foliations by caustics in strictly convex open billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1418-1467
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation