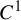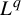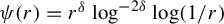Refine listing
Actions for selected content:
258 results in 37Dxx
Some hyperbolicity revisited and robust transitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 3800-3831
- Print publication:
- December 2025
-
- Article
- Export citation
Non-uniformly hyperbolic endomorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1313-1356
- Print publication:
- June 2025
-
- Article
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3698-3727
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vassiliev invariants and writhe for periodic orbits of Axiom A flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2659-2671
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical Diophantine approximation and shrinking targets for
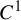 $C^{1}$ weakly conformal IFSs with overlaps
$C^{1}$ weakly conformal IFSs with overlaps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1777-1826
- Print publication:
- June 2025
-
- Article
- Export citation
Hölder continuity of measures for heavy tail potentials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 2476-2513
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL SYSTEMS ON SOME ELLIPTIC MODULAR SURFACES VIA OPERATORS ON LINE ARRANGEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 357-375
- Print publication:
- June 2025
-
- Article
- Export citation
A variational principle of scaled entropy for amenable group actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-28
-
- Article
- Export citation
Dichotomy spectrum and reducibility for mean hyperbolic systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-19
-
- Article
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
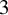 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The sectional curvature of the infinite dimensional manifold of Hölder equilibrium probabilities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 348-402
-
- Article
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal strong foliations in skew-products of iterated function systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2273-2313
- Print publication:
- August 2025
-
- Article
- Export citation
Quasidiagonals in strata of translation surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 2233-2248
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic data rigidity of Anosov automorphisms with Jordan blocks
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 1129-1160
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surfaces of section for geodesic flows of closed surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1698-1733
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1444-1460
- Print publication:
- May 2025
-
- Article
- Export citation