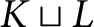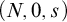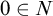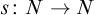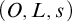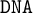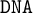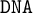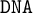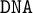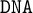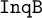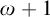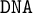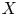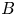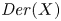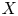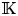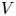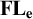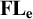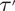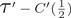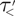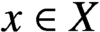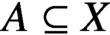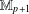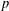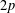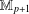Refine listing
Actions for selected content:
118 results in 08xxx
On the homotopy and strong homotopy type of complexes of discrete Morse functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 February 2022, pp. 19-37
- Print publication:
- March 2023
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ALGEBRAIC APPROACH TO INQUISITIVE AND
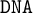 $\mathtt {DNA}$-LOGICS
$\mathtt {DNA}$-LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 950-990
- Print publication:
- December 2022
-
- Article
- Export citation
On free subalgebras of varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 89-101
-
- Article
- Export citation
ON EQUATIONAL COMPLETENESS THEOREMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1522-1575
- Print publication:
- December 2022
-
- Article
- Export citation
Algebras with representable representations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 555-573
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE POSET OF ALL LOGICS II: LEIBNIZ CLASSES AND HIERARCHY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 June 2021, pp. 324-362
- Print publication:
- March 2023
-
- Article
- Export citation
MOST SIMPLE EXTENSIONS OF
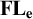 $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
- Print publication:
- September 2022
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
- Print publication:
- September 2021
-
- Article
- Export citation
CELLULAR AUTOMATA OVER ALGEBRAIC STRUCTURES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 306-319
- Print publication:
- May 2022
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
- Print publication:
- September 2021
-
- Article
- Export citation
MALTSEV CONDITIONS FOR GENERAL CONGRUENCE MEET-SEMIDISTRIBUTIVE ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1432-1451
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFINITARY COMMUTATIVITY AND ABELIANIZATION IN FUNDAMENTAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 289-311
- Print publication:
- June 2022
-
- Article
- Export citation
THE DISTRIBUTIVITY SPECTRUM OF BAKER’S VARIETY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 119-144
- Print publication:
- February 2021
-
- Article
- Export citation
THE FUNDAMENTAL THEOREM OF CENTRAL ELEMENT THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1599-1606
- Print publication:
- December 2020
-
- Article
- Export citation
DECIDING SOME MALTSEV CONDITIONS IN FINITE IDEMPOTENT ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 June 2020, pp. 539-562
- Print publication:
- June 2020
-
- Article
- Export citation
A MINIMAL CONGRUENCE LATTICE REPRESENTATION FOR
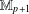 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 332-340
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
AXIOMATISABILITY OF THE CLASS OF MONOLITHIC GROUPS IN A VARIETY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 67-76
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Deciding the Existence of Minority Terms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 577-591
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation