It is shown that if V is a congruence distributive variety whose members have one element subalgebras, then the class of absolute retracts of V is closed under direct products. If V is residually small, then a characterisation of the amalgamation class of V is given.

We consider the lattice of pseudovarieties contained in a given pseudovariety P. It is shown that if the lattice L of subpseudovarieties of P has finite height, then L is isomorphic to the lattice of subvarieties of a locally finite variety. Thus not every finite lattice is isomorphic to a lattice of subpseudovarieties. Moreover, the lattice of subpseudovarieties of P satisfies every positive universal sentence holding in all lattice of subvarieties of varieties V(A) ganarated by algebras A ε P.

There are some well-known laws that the commutator satisfies in groups, and that go by some or all of the names Jacobi, Witt, Hall; and there are also some lesser-known laws. This is an attempt at an axiomatic study of the interdependence and independence of these laws.

An inverse semigroup S is said to be modular if its lattice 𝓛𝓕 (S) of inverse subsemigroups is modular. We show that it is sufficient to study simple inverse semigroups which are not groups. Our main theorem states that such a semigroup S is modular if and only if (I) S is combinatorial, (II) its semilattice E of idempotents is “Archimedean” in S, (III) its maximum group homomorphic image G is locally cyclic and (IV) the poset of idempotents of each 𝓓-class of S is either a chain or contains exactly one pair of incomparable elements, each of which is maximal. Thus in view of earlier results of the second author a simple modular inverse semigroup is “almost” distributive. The bisimple modular inverse semigroups are explicitly constructed. It is remarkable that exactly one of these is nondistributive.

A variant of Kurosh-Amitsur radical theory is developed for algebras with a collection of (finitary) operations ω, all of which are idempotent, that is satisfy the condition ω(x, x,…, x) = x. In such algebras, all classes of any congruence are subalgebras. In place of a largest normal radical subobject, a largest congruence with radical congruence classes is considered. In congruence-permutable varieties the parallels with conventional radical theory are most striking.

A category V is called universal (or binding) if every category of algebras is isomorphic to a full subcategory of V. The main result states that a semigroup variety V is universal if and only if it contains all commutative semigroups and fails the identity xnyn = (xy)n for every n ≥ 1. Further-more, the universality of a semigroup variety V is equivalent to the existence in V of a nontrivial semigroup whose endomorphism monoid is trivial, and also to the representability of every monoid as the monoid of all endomorphisms of some semigroup in V. Every universal semigroup variety contains a minimal one with this property while there is no smallest universal semigroup variety.

It is well-known that in any near-ring, any intersection of prime ideals is a semi-prime ideal. The aim of this note is to prove that any ideal is a prime ideal if and only if it is equal to its prime radical. As a consequence of this we have any semi-prime ideal I in a near-ring N is the intersection of minimal prime ideals of I in N and that I is the intersection of all prime ideals containing I.

Algebras (A, ∧, ∨, ~, γ, 0, 1) of type (2,2,1,1,0,0) such that (A, ∧, ∨, ~, γ 0, 1) is a De Morgan algebra and γ is a lattice homomorphism from A into its center that satisfies one of the conditions (i) a ≤ γa or (ii) a ≤ ~ a ∧ γa are considered. The dual categories and the lattice of their subvarieties are determined, and applications to Lukasiewicz algebras are given.

Given a universal algebra A, one can define for each positive integer n the set of functions on A which can be “interpolated” at any n elements of A by a polynomial function on A. These sets form a chain with respect to inclusion. It is known for several varieties that many of these sets coincide for all algebras A in the variety. We show here that, in contrast with these results, the coincident sets in the chain can to a large extent be specified arbitrarily by suitably choosing A from the variety of commutative semigroups.

It is well known that in any near-ring, any intersection of prime ideals is a semiprime ideal. The aim of this paper is to prove that any semiprime ideal I in a near-ring N is the intersection of all minimal prime ideals of I in N. As a consequence of this we have any seimprime ideal I is the intersectionof all prime ideals containing I.

We determine which varieties of commutative semigroups have the weak or strong amalgamation property. These are precisely the varieties of inflations of semilattices of abelian groups.

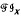In a previous paper ([14]) the author showed that a free inverse semigroup is determined by its lattice 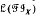of inverse subsemigroups, in the sense that for any inverse semigroup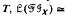 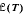T, implies 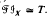. (In fact, the lattice isomorphism is induced by an isomorphism of upon T.) In this paper the results leading up to that theorem are generalized (from completely semisimple to arbitrary inverse semigroups) and applied to various classes, including simple, fundamental and E-unitary inverse semigroups. In particular it is shown that the free product of two groups in the category of inverse semigroups is determined by its lattice of inverse subsemigroups.

By a theorem of G. Birkhoff, every algebra in an equationally defined class of algebras K is a subdirect product of subdirectly irreducible algebras of K. In this paper we show that this result is true for any class of structures. not necessarily algebraic, closed under isomorphisms and direct limits. Quasivarieties in the sense of Malcev are examples of such classes of structures. This includes Birkhoffs result as a particular case.

Let J be a cofinite set of positive integers which contains 1. In (1973) I proved that the following condition on a variety (equational class) is Mal'tsev-definable: if υ ∈and υ is finite, then |υ| ∈J. This article contains some subsidiary results, concerned mainly with a more detailed description of these Mal'tsev conditions. Many of our results arose upon considering a recent article of W. D. Neumann (1978).

The main theorem of this paper shows that the lattice of congruences contained is some equivalence π on a semigroup S can be decomposed into a subdirect product of sublattices of the congruence lattices on the ‘prinipal π-facotrsρ of S—the semigroups formed by adjoining zeroes to the π-classes—whenever these are well-defined. The theorem is then applied to various equavalences and classes of semigroups to give some new results and alternative proofs of known ones.

In this paper we investigate near-rings of polynomials and polynomial functions. After some results which belong to universal algebra we turn our attention to the familiar case of polynomials and polynomial functions over a commutative ring with identity. We study the relation between ring- and near-ring homomorphisms, and the behaviour of polynomial near-rings when the ring splits into a direct sum. A discussion of the structure of these polynomial near-rings (radical, semisimplicity) finishes this paper. These investigations are motivated by Clay and Doi (1973).

Let P be a partially-ordered set in which every two elements have a common lower bound. It is proved that there exists a lower semilattice L whose elements are labelled with elements of P in such a way that (i) comparable elements of L are labelled with elements of P in the same strict order relation; (ii) each element of P is used as a label and every two comparable elements of P are labels of comparable elements of L; (iii) for any two elements of L with the same label, there is a label-preserving isomorphism between the corresponding principal ideals. Such a structure is called a full, uniform P-labelled semilattice.