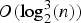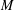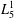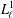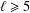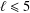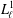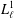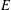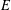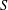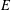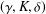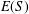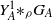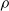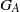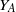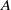Refine listing
Actions for selected content:
118 results in 08xxx
PROJECTIVE CLONE HOMOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 148-161
- Print publication:
- March 2021
-
- Article
- Export citation
CONTENT AND SINGLETONS BRING UNIQUE IDENTIFICATION MINORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 67-90
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Low Growth Equational Complexity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 197-210
-
- Article
- Export citation
LEE MONOIDS ARE NONFINITELY BASED WHILE THE SETS OF THEIR ISOTERMS ARE FINITELY BASED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 422-434
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
REFLECTORS AND GLOBALIZATIONS OF PARTIAL ACTIONS OF GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 358-379
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation
VARIETIES OF SKEW BOOLEAN ALGEBRAS WITH INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 290-306
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
DUALITY FOR QUASIPOLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 95-117
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
GROWTH RATES OF ALGEBRAS, I: POINTED CUBE TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 56-94
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
COMPLETE LATTICE HOMOMORPHISM OF STRONGLY REGULAR CONGRUENCES ON
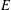 $E$-INVERSIVE SEMIGROUPS
$E$-INVERSIVE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 199-215
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
SUPERNILPOTENCE PREVENTS DUALIZABILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 September 2013, pp. 1-24
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON FREE SPECTRA OF A CLASS OF FINITE INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 March 2013, pp. 225-237
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
A universality result for endomorphism monoids of some ultrahomogeneous structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 635-656
-
- Article
-
- You have access
- Export citation
FREE ADEQUATE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 365-390
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Retracts of trees and free left adequate semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 731-747
-
- Article
-
- You have access
- Export citation
DUALIZABILITY OF GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 24 February 2011, pp. 377-392
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Independence algebras, basis algebras and semigroups of quotients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 697-729
-
- Article
-
- You have access
- Export citation
GROWTH OF GENERATING SETS FOR DIRECT POWERS OF CLASSICAL ALGEBRAIC STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2010, pp. 105-126
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
COMBINATORIAL REES–SUSHKEVICH VARIETIES THAT ARE CROSS, FINITELY GENERATED, OR SMALL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 13 August 2009, pp. 64-84
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
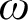
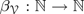
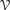 bounds the size of equation required to determine the membership of
bounds the size of equation required to determine the membership of 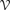 . Known examples of finitely generated varieties
. Known examples of finitely generated varieties 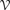 with unbounded equational complexity have growth in Ω(
with unbounded equational complexity have growth in Ω(