Refine listing
Actions for selected content:
118 results in 08xxx
DUALITY FOR CONVEX POLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 399-412
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
EVERY SHIFT AUTOMORPHISM VARIETY HAS AN INFINITE SUBDIRECTLY IRREDUCIBLE MEMBER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 19 January 2010, pp. 231-238
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
PRINCIPAL AND SYNTACTIC CONGRUENCES IN CONGRUENCE-DISTRIBUTIVE AND CONGRUENCE-PERMUTABLE VARIETIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 59-74
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
VARIETIES GENERATED BY COMPLETELY 0-SIMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 375-403
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Multialgebras, universal algebras and identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-140
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Free algebras in varieties of BL-algebras generated by a BLn-chain
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-439
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Optimal natural dualities: the role of endomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-296
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Relatively free algebras with weak exchange properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-384
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
The Direct Decomposition of l-algebras into Products of Subdirectly Irreducible Factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-56
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Transferring Optimal Dualities: Theory and Practice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-420
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Strong duality for metacyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-392
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Strong and full dualisability: three-element unary algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-220
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Some classes of pseudo-BL algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-154
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Free algebras in the variety of three-valued closure algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-198
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Nilpotent groups are not dualizable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-180
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Mono-unary algebras are strongly dualizable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-172
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Fregean subtractive varieties with definable congruence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-366
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Congruence quasi-orderability in subtractive varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-446
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Semidistributive inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-51
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Medial idempotent groupoids III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-320
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
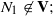 (iii)
(iii) 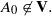 The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.
The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.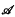 , generated by a finite algebra
, generated by a finite algebra 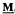 , has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on
, has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on 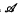 , an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when
, an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when 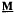 is a subdirectly irreducible lattice-structured algebra.
is a subdirectly irreducible lattice-structured algebra.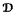 generated by a finite algebra
generated by a finite algebra 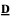 and assume that
and assume that 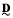 yields a natural duality on
yields a natural duality on 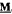 , which is also optimal modulo endormorphisms, for any finite algebra
, which is also optimal modulo endormorphisms, for any finite algebra 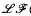 (
(