We study actions of Lie supergroups, in particular, the hitherto elusive notion of orbits through odd (or more general) points. Following categorical principles, we derive a conceptual framework for their treatment and therein prove general existence theorems for the isotropy (or stabiliser) supergroups and orbits through general points. In this setting, we show that the coadjoint orbits always admit a (relative) supersymplectic structure of Kirillov–Kostant–Souriau type. Applying a family version of Kirillov’s orbit method, we decompose the regular representation of an odd Abelian supergroup into an odd direct integral of characters and construct universal families of representations, parametrised by a supermanifold, for two different super variants of the Heisenberg group.

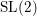We classify the horizontal $\text{SL}(2)$s and $\mathbb{R}$-split polarized mixed Hodge structures on a Mumford–Tate domain.

We consider the problem of deforming simultaneously a pair of given structures. We show that such deformations are governed by an $L_{\infty }$-algebra, which we construct explicitly. Our machinery is based on Voronov’s derived bracket construction. In this paper we consider only geometric applications, including deformations of coisotropic submanifolds in Poisson manifolds, of twisted Poisson structures, and of complex structures within generalized complex geometry. These applications cannot be, to our knowledge, obtained by other methods such as operad theory.

We prove a vanishing theorem for the twisted de Rham cohomology of a compact manifold.

We study the local symplectic algebra of curves. We use the method of algebraic restrictions to classify symplectic T7, T8 singularities. We define discrete symplectic invariants (the Lagrangian tangency orders) and compare them with the index of isotropy. We use these invariants to distinguish symplectic singularities of classical T7 singularity. We also give the geometric description of symplectic classes of the singularity.

This paper deals with 3-forms on six-dimensional manifolds, the first dimension where the classification of 3-forms is not trivial. It includes three classes of multisymplectic 3-forms. We study the class which is closely related to almost complex structures.

We give a formula for the character of the representation of the symmetric group Sn on each isotypic component of the cohomology of the set of regular elements of a maximal torus of SLn, with respect to the action of the centre.

We introduce complex differential geometry twisted by a real line bundle. This provides a new approach to understand the various real objects that are associated with an anti-holomorphic involution. We also generalize a result of Greenleaf about real analytic sheaves from dimension 2 to higher dimensions.

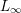
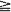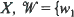We present a systematic method of approximating, to an arbitrary accuracy, a probability measure µ on x = [0,1]q, q 1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on , w2, · ·· }, subject to an ‘ϵ-contractivity' condition, is employed. Thus, only an optimization over the associated probabilities pi is required. 2. We prove a collage theorem for moments which reduces the moment matching problem to that of minimizing the collage distance between moment vectors. The minimization procedure is a standard quadratic programming problem in the pi which can be solved in a finite number of steps. Some numerical calculations for the approximation of measures on [0, 1] are presented.

The aim of this paper is to give a clear statement, and, I hope, a reasonably clear proof, of a theorem of Thorn, which occurs in his important and difficult paper “Ensembles et morphismes stratifiés” [10]. The theorem to which I refer is Théorème 1.D.1 of [10]. “Tout espace stratifié compact admet une présentation associée aux applications kYX données”. At least, I think that the theorem herein described is equivalent to the above, but I could not swear to it. The main difficulty is that, despite strenuous efforts on my part, I have always found it easier to rig up my own system of definitions than to work within the framework suggested by Thorn. However, the two accounts clearly say the same sort of thing. In particular, §1 of the present paper is closely related to, and heavily influenced by, the material on page 250 of [10].