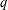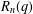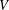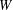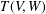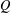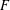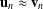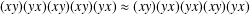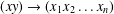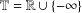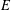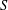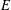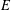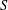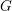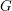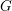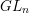Refine listing
Actions for selected content:
285 results in 20Mxx
REGULAR SEMIGROUPS WITH NORMAL IDEMPOTENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 116-125
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation
THE ANNIHILATOR OF TENSOR SPACE IN THE
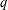 $q$ -ROOK MONOID ALGEBRA
$q$ -ROOK MONOID ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 77-86
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
THE REGULAR PART OF A SEMIGROUP OF LINEAR TRANSFORMATIONS WITH RESTRICTED RANGE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 402-419
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Von Neumann Algebras and Extensions of Inverse Semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 57-97
-
- Article
- Export citation
A NOTE ON THE HOWSON PROPERTY IN INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 457-463
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
The genus, Frobenius number and pseudo-Frobenius numbers of numerical semigroups of type 2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1081-1090
- Print publication:
- October 2016
-
- Article
- Export citation
GROWTHS OF ENDOMORPHISMS OF FINITELY GENERATED SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 163-184
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Free Monoids are Coherent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 127-131
-
- Article
- Export citation
EMBEDDING IN A FINITE 2-GENERATOR SEMIGROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 61-75
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
REALIZABILITY PROBLEM FOR COMMUTING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 335-355
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Numerical semigroups with a given set of pseudo-Frobenius numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 186-205
-
- Article
-
- You have access
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
ON THE TOTAL COMPONENT OF THE PARTIAL SCHUR MULTIPLIER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 374-402
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 54-64
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A SUFFICIENT CONDITION UNDER WHICH A SEMIGROUP IS NONFINITELY BASED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 454-466
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
COMPLETE LATTICE HOMOMORPHISM OF STRONGLY REGULAR CONGRUENCES ON
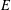 $E$-INVERSIVE SEMIGROUPS
$E$-INVERSIVE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 199-215
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Compactifications of reductive groups as moduli stacks of bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 62-98
- Print publication:
- January 2016
-
- Article
- Export citation